15 Données déséquilibrées

Données déséquilibrées et modèle logistique

df <- data.frame(MALADE=c(208,42),
                 NON_MALADE=c(48,202),
                 FUMEUR=c("OUI","NON"))
model <- glm(cbind(MALADE,NON_MALADE)~FUMEUR,data=df,family=binomial)
coef(model)

(Intercept)   FUMEUROUI 
  -1.570598    3.036935 

newX <- data.frame(FUMEUR=c("OUI","NON"))
rownames(newX) <- c("OUI","NON")
predict(model,newdata = newX,type="response")

      OUI       NON 
0.8125000 0.1721311 

beta1_cor <- coef(model)[1]-log(0.995/0.005)
beta2 <- coef(model)[2]

exp(beta1_cor+beta2)/(1+exp(beta1_cor+beta2))

(Intercept) 
 0.02131148 

exp(beta1_cor)/(1+exp(beta1_cor))

(Intercept) 
0.001043738 

tau <- c(0.05,0.95)
ind0 <- which(df$Y==0)
ind1 <- which(df$Y==1)
choix0 <- sample(ind0, size=length(ind0)*tau[1], replace = F)
choix1 <- sample(ind1, size=length(ind1)*tau[2], replace = F)
dff <- rbind(df[choix0,], df[choix1,])

mod <- glm(Y~., data=dff, family="binomial")

gamma <- coef(mod)
gamma[1] - log(tau[2]/tau[1])

glm(Y~. + offset(rep(log(tau[2]/tau[1]), nrow(dff))),
    data=dff, family="binomial")

Stratégies pour données déséquilibrées

Quelques méthodes de rééquilibrage

library(tidyverse)

set.seed(123458)
n1 <- 10
X11 <- runif(n1,0,0.25)
X21 <- runif(n1,0,1)
X12 <- runif(n1,0,1)
X22 <- runif(n1,0.75,1)
n2 <- 80
X13 <- runif(n2,0.25,1)
X23 <- runif(n2,0,0.75)
X1 <- c(X11,X12,X13)
X2 <- c(X21,X22,X23)
Y <- c(rep(1,2*n1),rep(0,n2)) %>% as.factor()
df <- data.frame(X1,X2,Y,id=as.character(1:100))
df$Y[c(1,16)] <- 0
#df$Y[c(41,48,59)] <- 1
df$Y[c(41,48)] <- 1
df <- df[,1:3]
ggplot(df)+aes(x=X1,y=X2)+geom_point(aes(color=Y))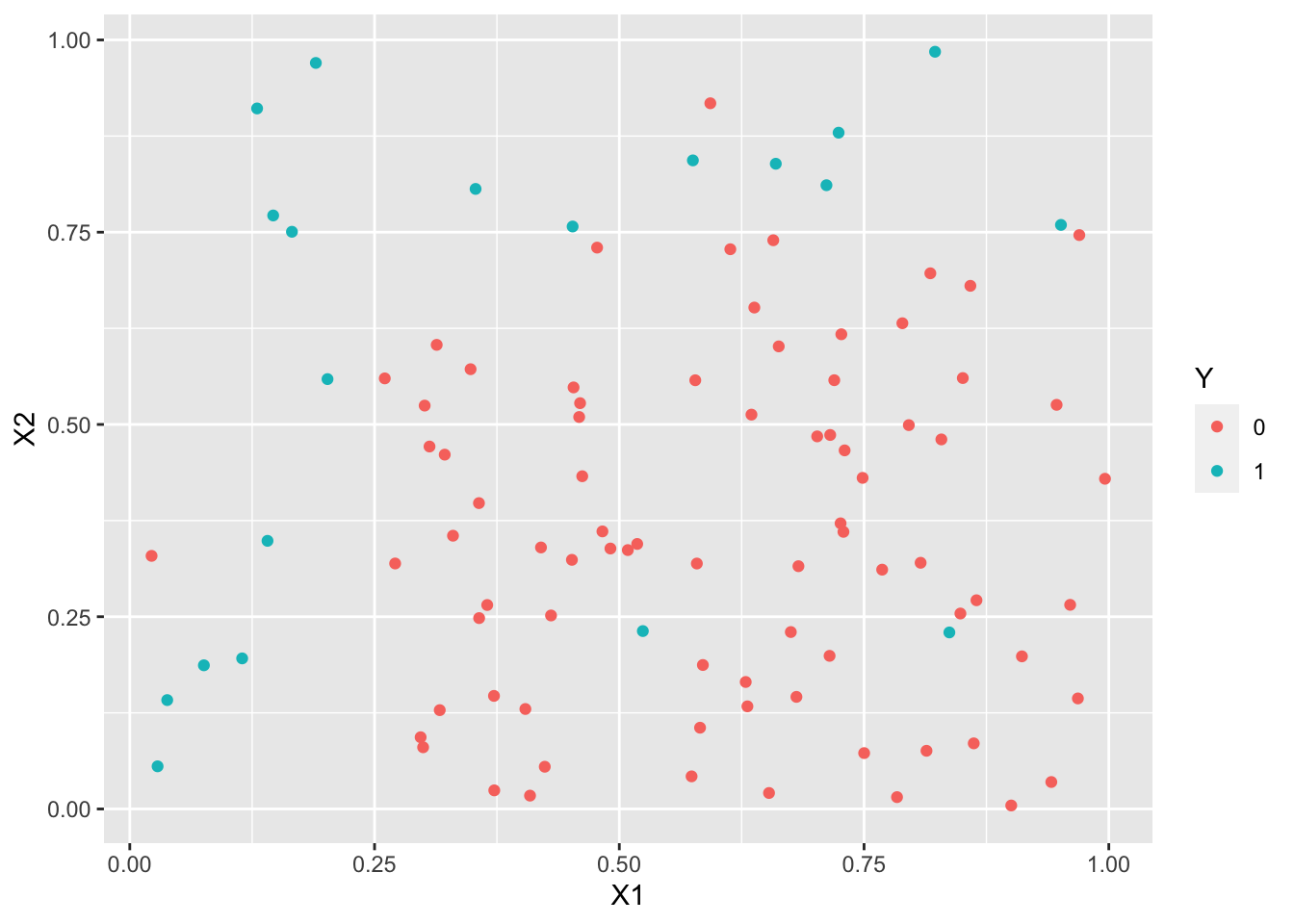

library(UBL)
over1 <- RandOverClassif(Y~., dat=df)
over2 <- RandOverClassif(Y~., dat=df, C.perc=list("0"=1,"1"=2))
summary(over1$Y)

 0  1 
80 80 

summary(over2$Y)

 0  1 
80 40 

set.seed(1234)
smote1 <- SmoteClassif(Y~.,dat=df,k=4)
smote2 <- SmoteClassif(Y~.,dat=df,k=4,C.perc=list("0"=1,"1"=2))
summary(smote1$Y)

 0  1 
50 50 

summary(smote2$Y)

 0  1 
80 40 

newsm1 <- anti_join(smote1,df)
newsm2 <- anti_join(smote2,df)
newsm <- bind_rows("smote1"=newsm1,"smote2"=newsm2,.id="algo")

df3 <- bind_rows("smote1"=smote1,"smote2"=smote2,.id="algo")
ggplot(df3)+aes(x=X1,y=X2,color=Y)+geom_point(aes(shape=Y),size=1.5)+facet_wrap(~algo)+
  geom_point(data=newsm,shape=1,size=4) + theme(legend.position='none')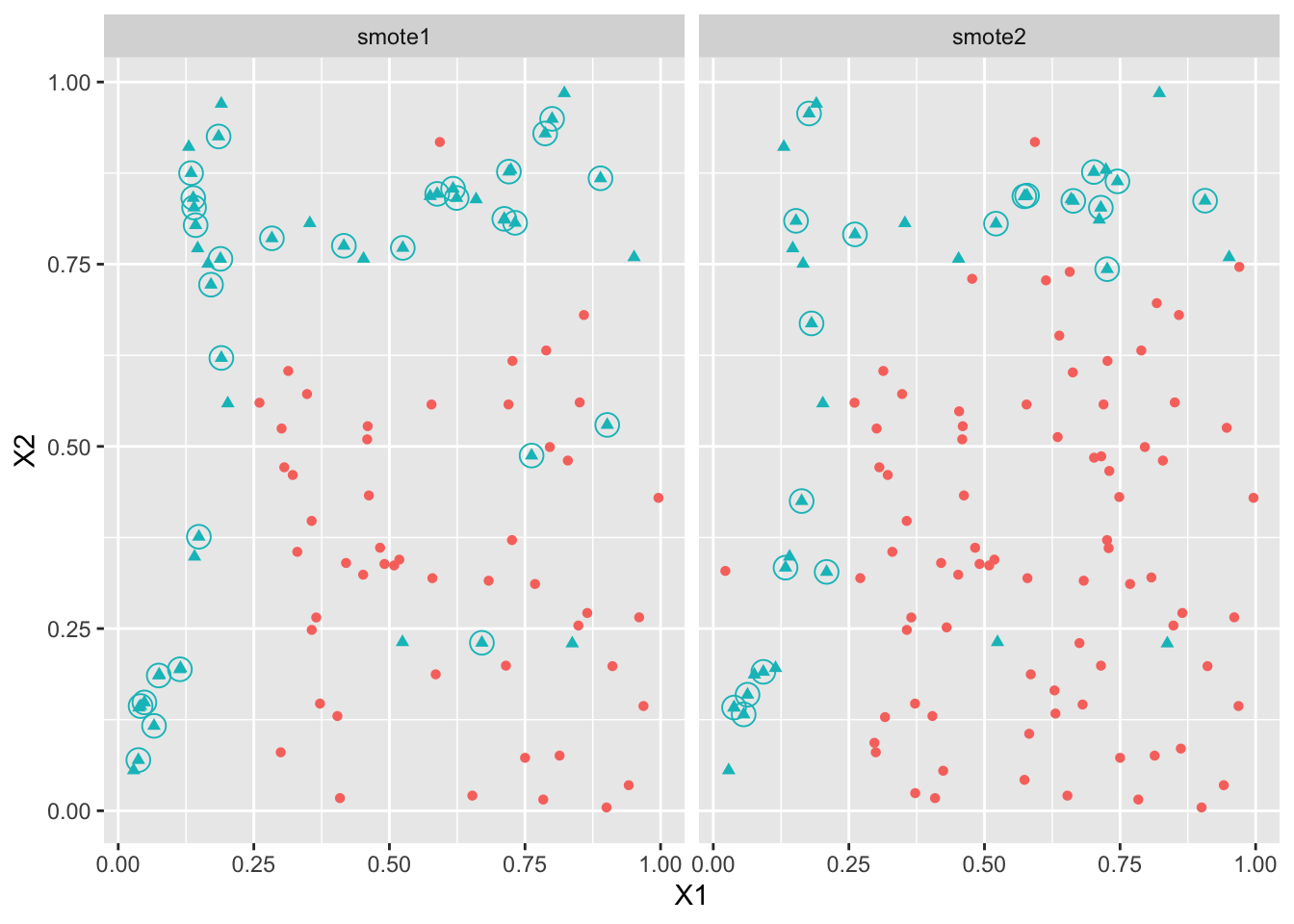

under1 <- RandUnderClassif(Y~.,dat=df)
under2 <- RandUnderClassif(Y~.,dat=df,C.perc=list("0"=0.5,"1"=1))
summary(under1$Y)

 0  1 
20 20 

summary(under2$Y)

 0  1 
40 20 

tomek1 <- TomekClassif(Y~.,dat=df)
tomek2 <- TomekClassif(Y~.,dat=df,rem="maj")
tomek1[[2]]

[1]   1   7  12  69  14 100  16  17

tomek2[[2]]

[1]   1  69 100  16

ind1 <- tomek1[[2]]
ind2 <- tomek2[[2]]
XS1 <- df[ind1,]
XS2 <- df[ind2,]
XS <- bind_rows("tomek1"=XS1,"tomek2"=XS2,.id="algo")
df5 <- bind_rows("tomek1"=df,"tomek2"=df,.id="algo")
ggplot(df5)+aes(x=X1,y=X2,color=Y)+geom_point(aes(color=Y,shape=Y),size=1.5)+facet_wrap(~algo)+
  geom_point(data=XS,shape=1,size=4) + theme(legend.position='none')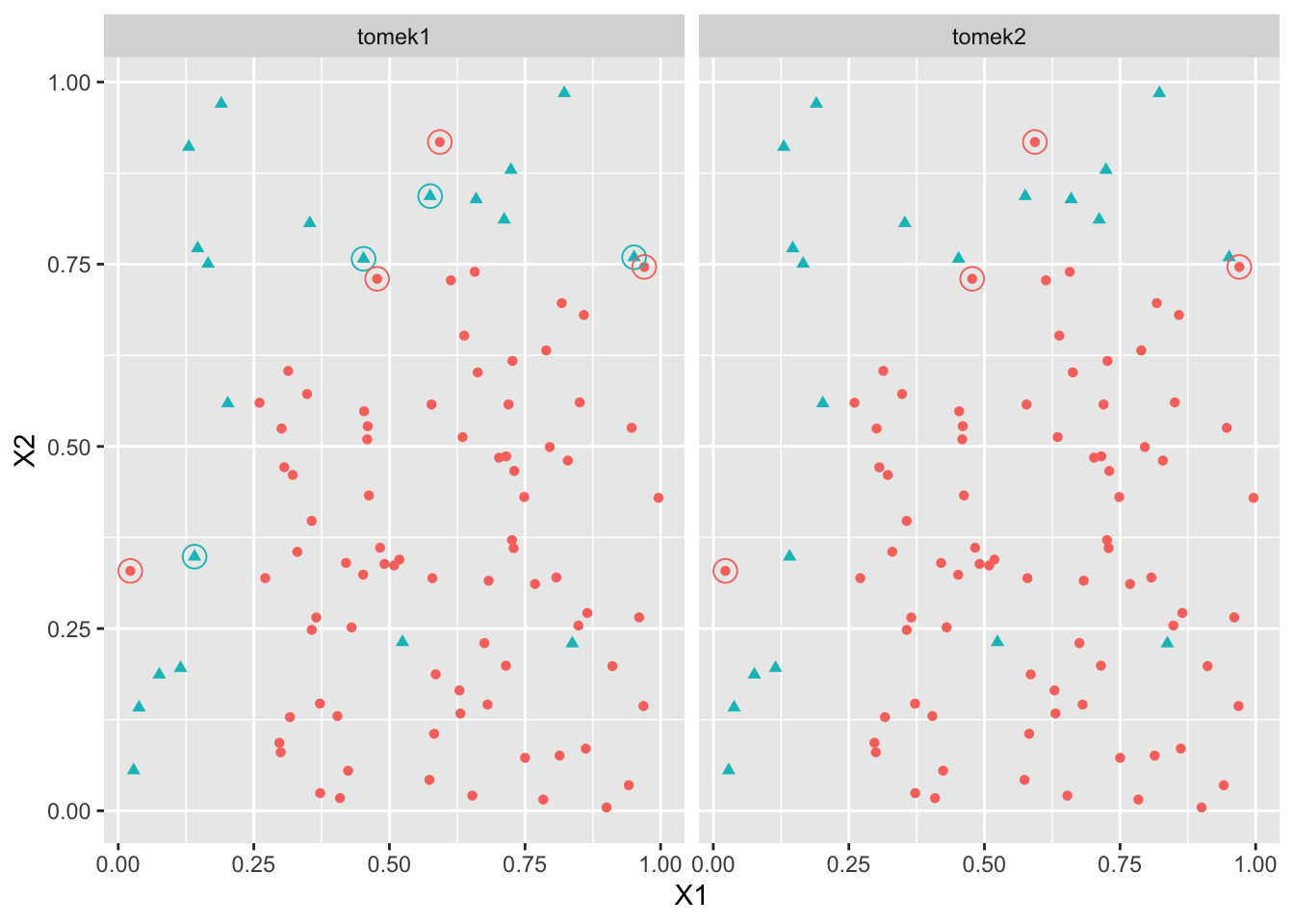

Critères pour données déséquilibrées

   P1
Y     0   1
  0 468   0
  1  31   1

   P2
Y     0   1
  0 407  61
  1   4  28

library(yardstick)
df <- data.frame(Y,P2)
multi_metric <- metric_set(accuracy,bal_accuracy,f_meas,kap)
multi_metric(df,truth=Y,estimate=P2,event_level = "second")

# A tibble: 4 × 3
  .metric      .estimator .estimate
  <chr>        <chr>          <dbl>
1 accuracy     binary         0.87 
2 bal_accuracy binary         0.872
3 f_meas       binary         0.463
4 kap          binary         0.407

Choisir un algorithme de rééquilibrage

Application aux données d’images publicitaires

summary(ad.data1$Y)

   ad. nonad. 
   459   2820 

ad.data1 <- ad.data1 %>% 
  transform(Y=fct_recode(Y,"0"="nonad.","1"="ad.")) %>% 
  transform(Y=fct_inseq(Y))

set.seed(1234)
bloc <- sample(1:10,nrow(ad.data1),replace=TRUE)
table(bloc)

bloc
  1   2   3   4   5   6   7   8   9  10 
309 327 329 310 358 354 304 337 342 309 

score <- data.frame(matrix(0,nrow=nrow(ad.data1),ncol=3))
names(score) <- c("logit","lasso","ridge")
SCORE <- list(brute=score,over=score,smote=score,under=score,tomek=score)

set.seed(4321)
library(glmnet)
score <- data.frame(matrix(0,nrow=nrow(ad.data1),ncol=3))
names(score) <- c("logit","lasso","ridge")
SCORE <- list(brute=score,over=score,smote=score,under=score,tomek=score)

for (k in 1:10){
  print(k)
  ind.test <- bloc==k
  dapp <- ad.data1[!ind.test,]
  dtest <- ad.data1[ind.test,]
  X.test <- model.matrix(Y~.,data=dtest)[,-1]
  
  ech.app <- list(norm=dapp,
                  over=RandOverClassif(Y~.,dat=dapp),
                  smote=SmoteClassif(Y~.,dat=dapp),
                  under=RandUnderClassif(Y~.,dat=dapp),
                  tomek=TomekClassif(Y~.,dat=dapp)[[1]])

  mod.mat.list <- function(df){model.matrix(Y~.,data=df)[,-1]}
  Y.list <- function(df) df$Y 
  
  X.app <- lapply(ech.app,mod.mat.list)
  Y.app <- lapply(ech.app,Y.list)
  
  for (j in 1:5){
    print(j)
    lasso <- cv.glmnet(X.app[[j]],Y.app[[j]],family="binomial")
    ridge <- cv.glmnet(X.app[[j]],Y.app[[j]],family="binomial",alpha=0)
    logit <- glm(Y~.,data=ech.app[[j]],family="binomial")
    SCORE[[j]][ind.test,] <- data.frame(
      logit=predict.glm(logit,newdata=dtest,type="response"),
      lasso=as.vector(predict(lasso,newx=X.test,type="response")),
      ridge=as.vector(predict(ridge,newx=X.test,type="response"))
    )
  }
}

mat.score <- bind_rows(brutes=SCORE[[1]],
                       over=SCORE[[2]],
                       smote=SCORE[[3]],
                       under=SCORE[[4]],
                       tomek=SCORE[[5]],.id="meth") %>% 
  mutate(obs=rep(ad.data1$Y,5))  %>% 
  pivot_longer(c(logit,lasso,ridge),
               names_to = "algo",values_to = "score")

mat.score %>% group_by(meth,algo) %>% 
  roc_auc(truth = obs,score,event_level = "second") %>%
  pivot_wider(-c(.metric,.estimator),
              names_from = algo,values_from = .estimate)

# A tibble: 5 × 4
  meth   lasso logit ridge
  <chr>  <dbl> <dbl> <dbl>
1 brutes 0.943 0.831 0.980
2 over   0.973 0.790 0.977
3 smote  0.973 0.680 0.977
4 tomek  0.950 0.763 0.979
5 under  0.956 0.787 0.964

mat.score <- mat.score %>% mutate(prev=as.factor(round(score)))

• Accuracy :

  mat.score %>% 
    group_by(meth,algo) %>% 
    accuracy(truth = obs,prev) %>%
    pivot_wider(names_from = algo,values_from = .estimate) %>%
    select(-(2:3))

  # A tibble: 5 × 4
    meth   lasso logit ridge
    <chr>  <dbl> <dbl> <dbl>
  1 brutes 0.969 0.886 0.970
  2 over   0.961 0.847 0.963
  3 smote  0.960 0.699 0.960
  4 tomek  0.969 0.818 0.970
  5 under  0.954 0.808 0.955

• Balanced accuracy :

  mat.score %>% 
    group_by(meth,algo) %>% 
    bal_accuracy(truth = obs,prev) %>%
    pivot_wider(names_from = algo,values_from = .estimate) %>%
    select(-(2:3))

  # A tibble: 5 × 4
    meth   lasso logit ridge
    <chr>  <dbl> <dbl> <dbl>
  1 brutes 0.898 0.832 0.900
  2 over   0.931 0.806 0.935
  3 smote  0.933 0.680 0.933
  4 tomek  0.896 0.797 0.900
  5 under  0.921 0.792 0.899

• F1 score :

  mat.score %>% 
    group_by(meth,algo) %>% 
    f_meas(truth = obs,prev,event_level = "second") %>%
    pivot_wider(names_from = algo,values_from = .estimate) %>%
    select(-(2:3))

  # A tibble: 5 × 4
    meth   lasso logit ridge
    <chr>  <dbl> <dbl> <dbl>
  1 brutes 0.879 0.650 0.884
  2 over   0.864 0.579 0.873
  3 smote  0.863 0.378 0.862
  4 tomek  0.876 0.542 0.882
  5 under  0.843 0.529 0.837

• Kappa de Cohen :

  mat.score %>% 
    group_by(meth,algo) %>% 
    kap(truth = obs,prev) %>%
    pivot_wider(names_from = algo,values_from = .estimate) %>%
    select(-(2:3))

  # A tibble: 5 × 4
    meth   lasso logit ridge
    <chr>  <dbl> <dbl> <dbl>
  1 brutes 0.862 0.584 0.867
  2 over   0.842 0.491 0.851
  3 smote  0.839 0.224 0.838
  4 tomek  0.859 0.440 0.866
  5 under  0.816 0.422 0.811

grille.score(mat.score,nom_algo="ridge",meth="norm")

# A tibble: 11 × 7
   seuil  sens  spec accuracy bal_accuracy f_meas   kap
   <chr> <dbl> <dbl>    <dbl>        <dbl>  <dbl> <dbl>
 1 0     1     0        0.14         0.5    0.246 0    
 2 0.1   0.955 0.671    0.711        0.813  0.48  0.343
 3 0.2   0.932 0.745    0.771        0.839  0.533 0.416
 4 0.3   0.911 0.851    0.86         0.881  0.645 0.566
 5 0.4   0.885 0.918    0.913        0.901  0.74  0.69 
 6 0.5   0.843 0.983    0.964        0.913  0.867 0.846
 7 0.6   0.797 0.991    0.964        0.894  0.861 0.841
 8 0.7   0.739 0.995    0.959        0.867  0.834 0.811
 9 0.8   0.672 0.997    0.952        0.835  0.796 0.77 
10 0.9   0.562 0.999    0.938        0.78   0.717 0.685
11 1     0     1        0.86         0.5   NA     0    

grille.score(mat.score,nom_algo="ridge",meth="over")

# A tibble: 11 × 7
   seuil  sens  spec accuracy bal_accuracy f_meas   kap
   <chr> <dbl> <dbl>    <dbl>        <dbl>  <dbl> <dbl>
 1 0     1     0        0.14         0.5    0.246 0    
 2 0.1   0.955 0.671    0.711        0.813  0.48  0.343
 3 0.2   0.932 0.745    0.771        0.839  0.533 0.416
 4 0.3   0.911 0.851    0.86         0.881  0.645 0.566
 5 0.4   0.885 0.918    0.913        0.901  0.74  0.69 
 6 0.5   0.843 0.983    0.964        0.913  0.867 0.846
 7 0.6   0.797 0.991    0.964        0.894  0.861 0.841
 8 0.7   0.739 0.995    0.959        0.867  0.834 0.811
 9 0.8   0.672 0.997    0.952        0.835  0.796 0.77 
10 0.9   0.562 0.999    0.938        0.78   0.717 0.685
11 1     0     1        0.86         0.5   NA     0    

grille.score(mat.score,nom_algo="ridge",meth="smote")

# A tibble: 11 × 7
   seuil  sens  spec accuracy bal_accuracy f_meas   kap
   <chr> <dbl> <dbl>    <dbl>        <dbl>  <dbl> <dbl>
 1 0     1     0        0.14         0.5    0.246 0    
 2 0.1   0.955 0.671    0.711        0.813  0.48  0.343
 3 0.2   0.932 0.745    0.771        0.839  0.533 0.416
 4 0.3   0.911 0.851    0.86         0.881  0.645 0.566
 5 0.4   0.885 0.918    0.913        0.901  0.74  0.69 
 6 0.5   0.843 0.983    0.964        0.913  0.867 0.846
 7 0.6   0.797 0.991    0.964        0.894  0.861 0.841
 8 0.7   0.739 0.995    0.959        0.867  0.834 0.811
 9 0.8   0.672 0.997    0.952        0.835  0.796 0.77 
10 0.9   0.562 0.999    0.938        0.78   0.717 0.685
11 1     0     1        0.86         0.5   NA     0