16 Introduction à la régression spline

ozone <- read.table("../donnees/ozone_simple.txt",header=T,sep=";")

polyreg <- function(donnee,d=3){
  sigmax <- sd(donnee[,"T12"])
  grillex <- seq(min(donnee[,"T12"])-sigmax,max(donnee[,"T12"])+sigmax,length=100)
  aprevoir <- data.frame(T12=grillex)
  regpol <- lm(O3~poly(T12,degree=d,raw=TRUE),data=donnee)
  prev <- predict(regpol,aprevoir)
  return(list(grillex=grillex,grilley=prev))
}

plot(O3~T12,data=ozone,xlab="T12",ylab="O3",xlim=c(0,35), ylim=c(0,150))
iter <- 1
for(ii in c(1,2,3,9)){
 tmp <- polyreg(ozone,d=ii)
 lines(tmp$grillex,tmp$grilley,col=iter,lty=iter)
 iter <- iter+1
}
legend("topleft",c("d=1","d=2","d=3","d=9"),col=1:4,lty=1:4)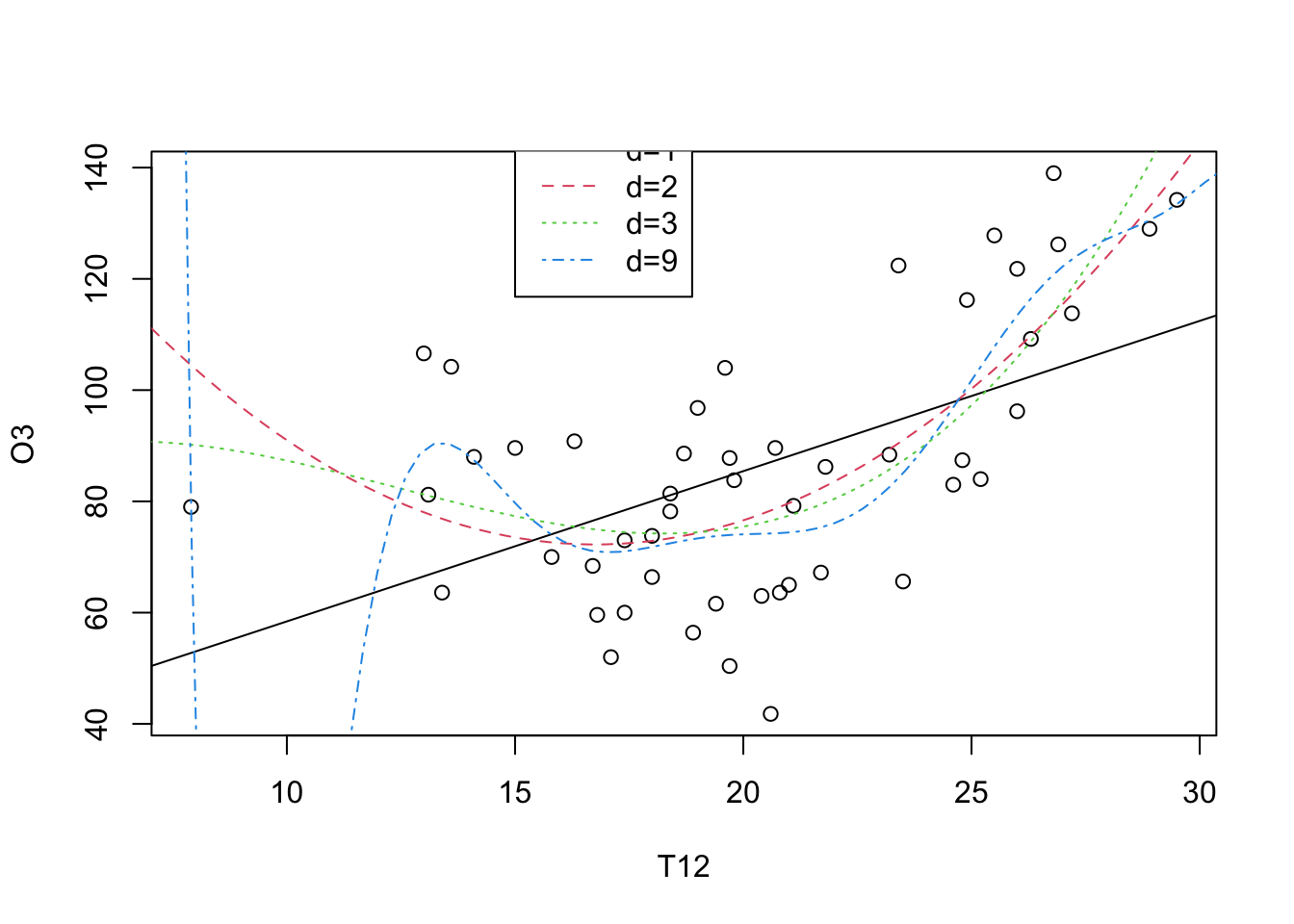

ind <- which(ozone[,2]<23)
regd <- lm(O3~T12,data=ozone[ind,])
regf <- lm(O3~T12,data=ozone[-ind,])
gxd <- seq(3,23,length=50)
gyd <- regd$coef[1]+gxd*regd$coef[2]
gxf <- seq(23,35,length=50)
gyf <- regf$coef[1]+gxf*regf$coef[2]
plot(O3~T12,data=ozone)
lines(gxd,gyd,col=2,lty=1,lwd=2)
lines(gxf,gyf,col=2,lty=1,lwd=2)
abline(v=23)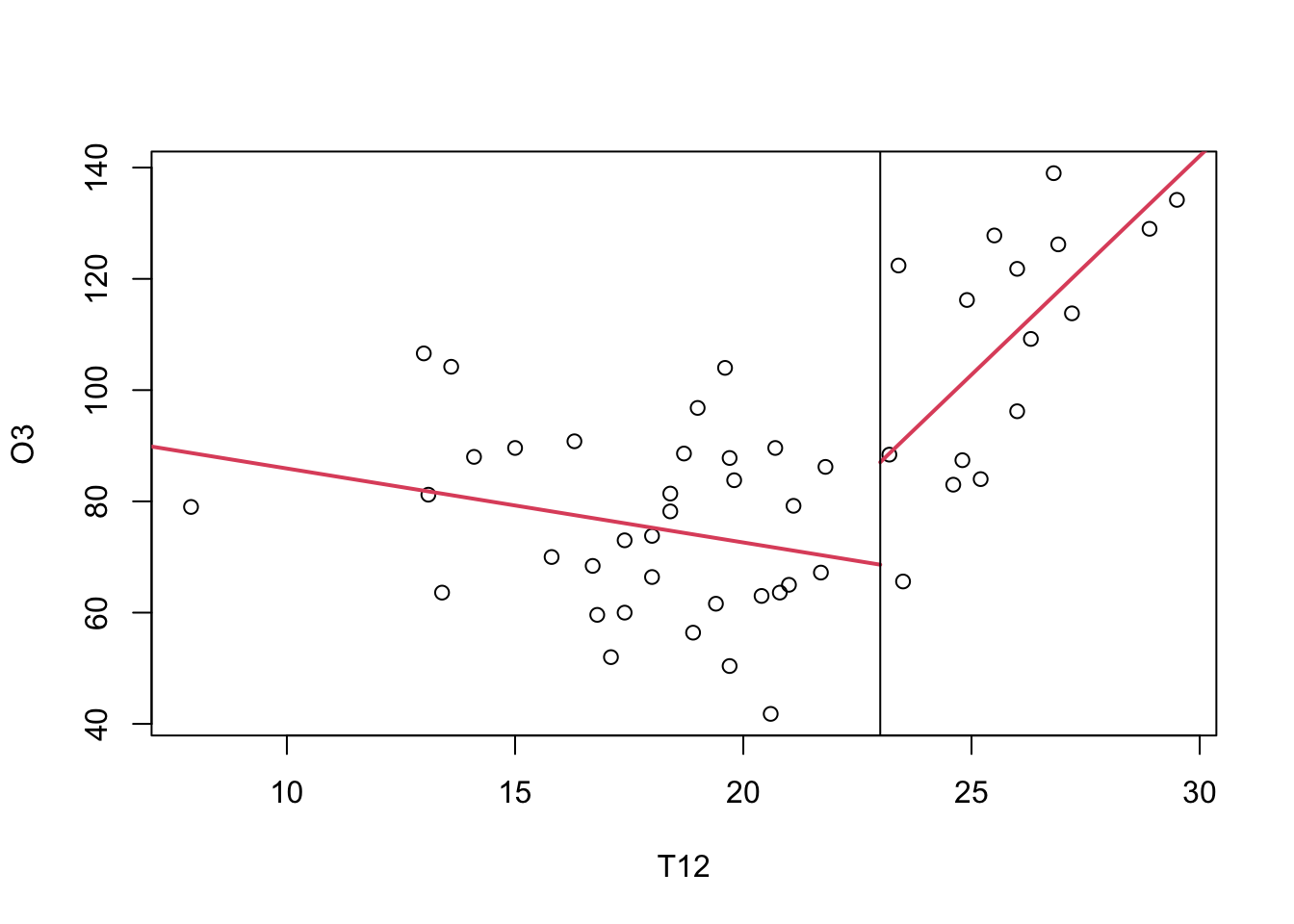

library(splines)
XB <- bs(ozone[,2], knots=c(15,23), degree=2,Boundary.knots=c(5,32))
regs <- lm(ozone[,"O3"] ~ XB)
regs$coef

(Intercept)         XB1         XB2         XB3         XB4 
  51.101947   61.543761    5.562286   70.459103  106.711539 

grillex <- seq(5,32,length=100)
bgrillex <- bs(grillex, knots=c(15,23), degree=2,Boundary.knots=c(5,32))
prev <- bgrillex%*%as.matrix(regs$coeff[-1])+regs$coeff[1]
plot(O3~T12,data=ozone)
lines(grillex,prev,col=2)
abline(v=c(15,23))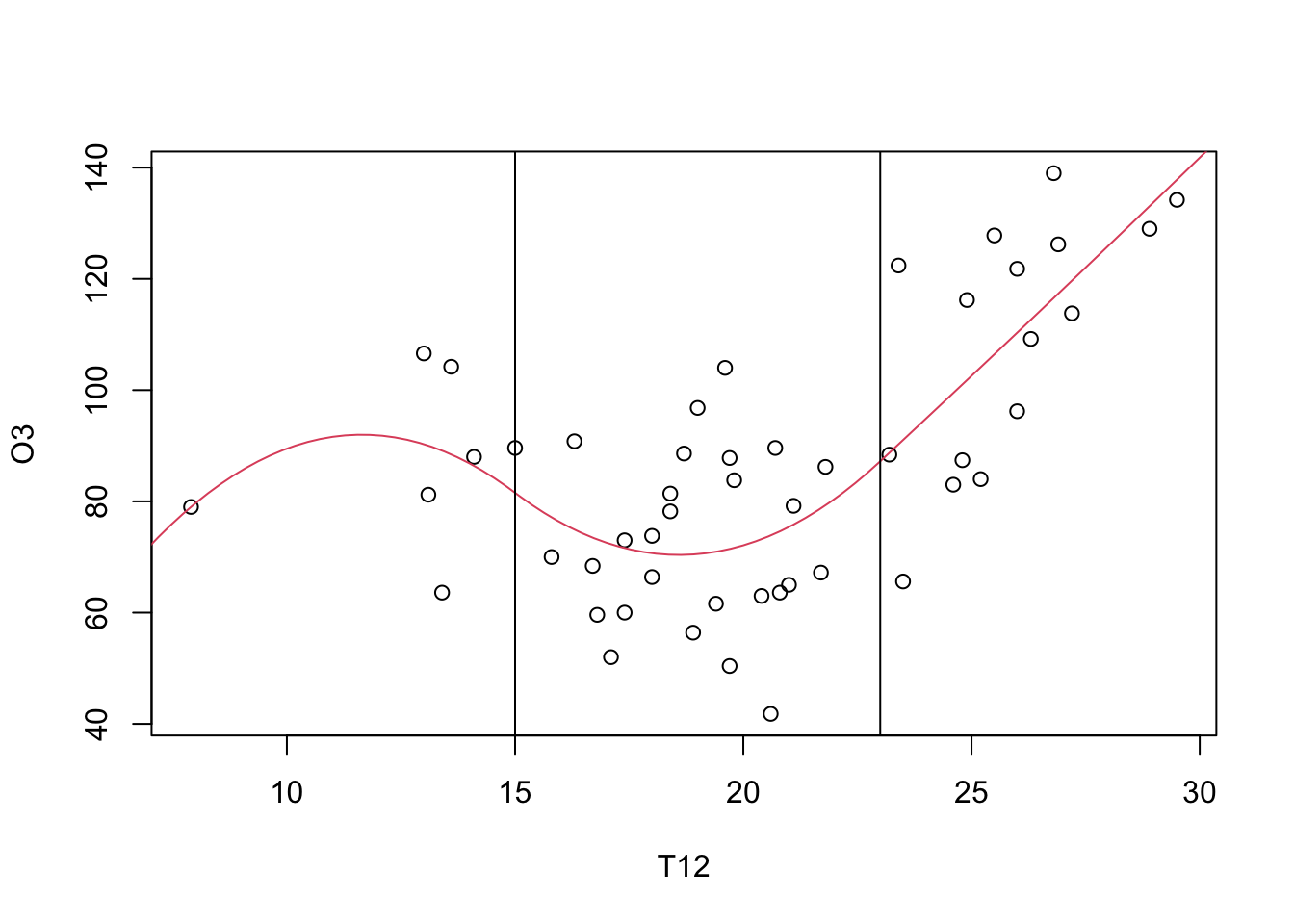

regssplinel1 <- smooth.spline(ozone[,2],ozone[,1],lambda =100)
prevl1 <- predict(regssplinel1,grillex)
plot(O3~T12,data=ozone)
lines(prevl1$x,prevl1$y,col=2)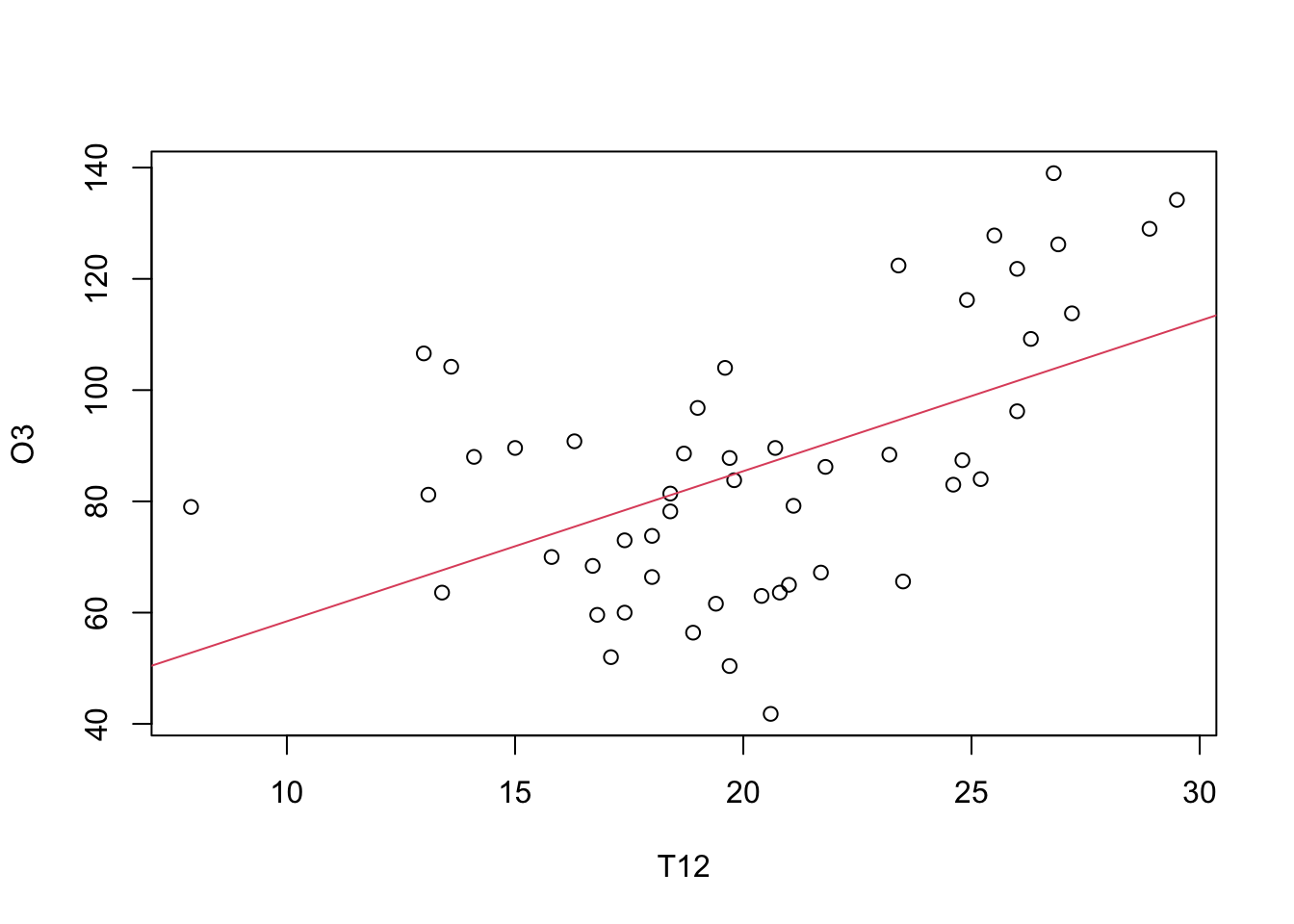

regsspline <- smooth.spline(ozone[,2],ozone[,1])
prev <- predict(regsspline,grillex)
plot(O3~T12,data=ozone)
lines(prev$x,prev$y,col=2)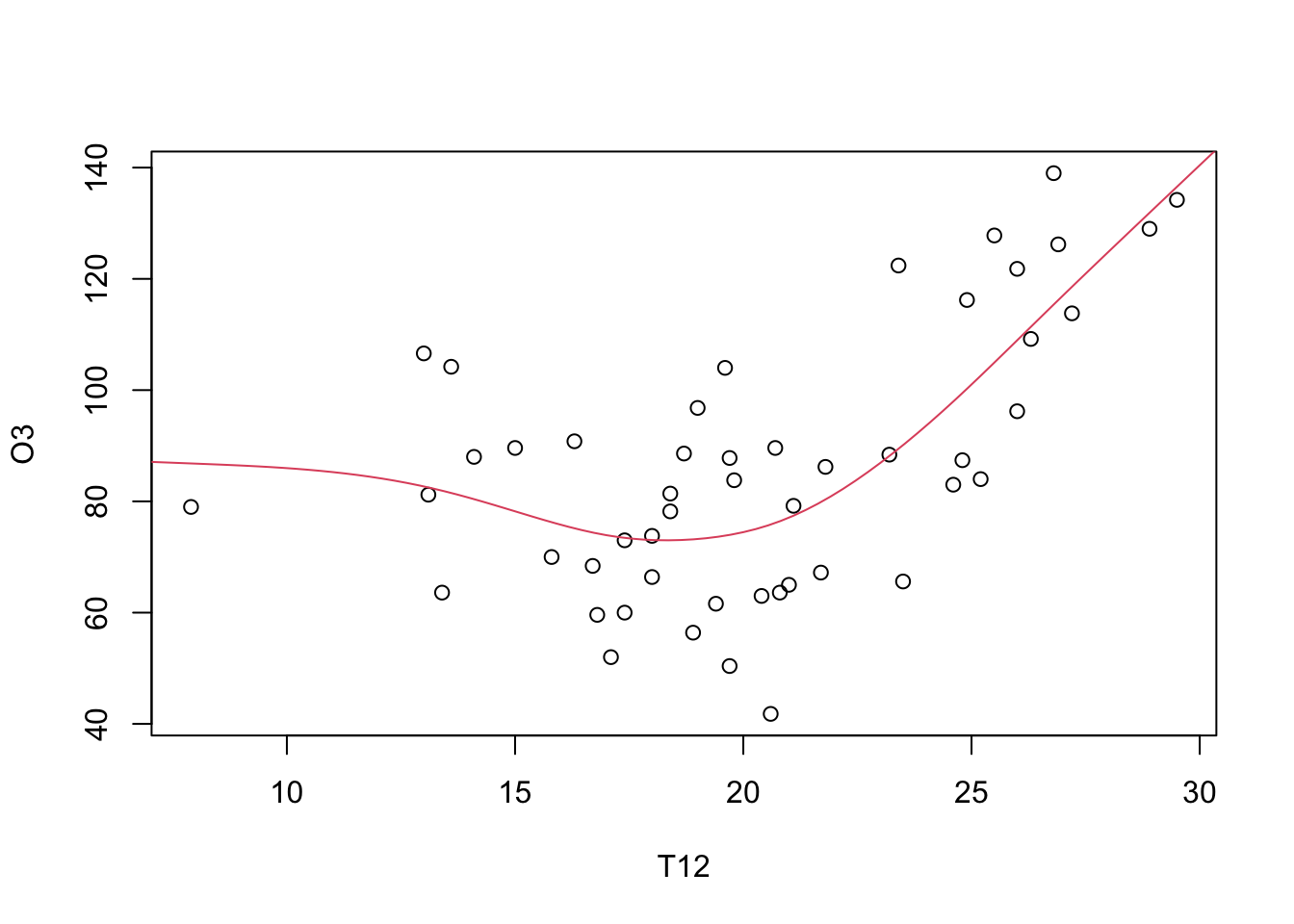

regsspline

Call:
smooth.spline(x = ozone[, 2], y = ozone[, 1])

Smoothing Parameter  spar= 0.9410342  lambda= 0.006833357 (15 iterations)
Equivalent Degrees of Freedom (Df): 4.156771
Penalized Criterion (RSS): 11036.88
GCV: 289.8012