16 Introduction à la régression spline
Exercice 1 (Questions de cours)
- C
- A
- A
- B
Exercice 2 (Fonction polyreg)
On importe les données
ozone <- read.table("../donnees/ozone_simple.txt",header=T,sep=";") sdT12 <- sd(ozone$T12)On crée la grille
grillex <- seq(min(ozone$T12)-sdT12,max(ozone$T12)+sdT12, length =100)On transforme en data frame
df <- data.frame(T12=grillex)On effectue une régression polynomiale de degré 3
basepoly <- poly(ozone$T12,degree=3,raw=T) newval <- predict(basepoly,df$T12) dfpoly <- data.frame(O3=ozone$O3,basepoly) regpoly <- lm(O3~.,data=dfpoly)On prévoit sur une grille
dfnewval <- data.frame(newval) prev <- predict(regpoly,dfnewval) plot(O3~T12,data=ozone) lines(grillex,prev,col=2)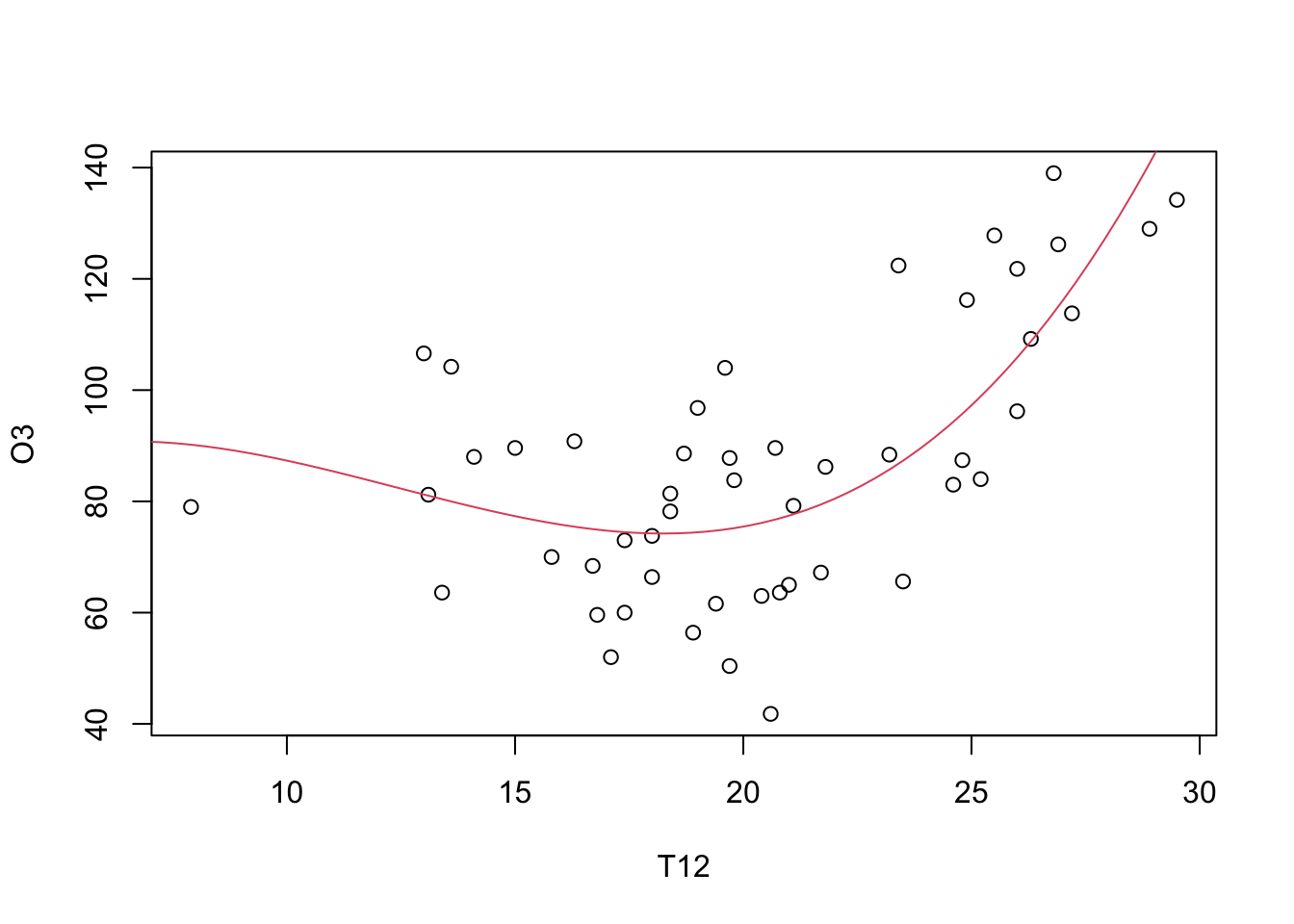
Création de la fonction
polyreg <- function(ozone,degre=3){ sdT12 <- sd(ozone$T12) grillex <- seq(min(ozone$T12)-sdT12,max(ozone$T12)+sdT12, length =100) df <- data.frame(T12=grillex) basepoly <- poly(ozone$T12,degree=3,raw=T) newval <- predict(basepoly,df$T12) dfpoly <- data.frame(O3=ozone$O3,basepoly) regpoly <- lm(O3~.,data=dfpoly) dfnewval <- data.frame(newval) prev <- predict(regpoly,dfnewval) return(list(grillex,prev)) }
Exercice 3 On applique la fonction précédente
ozone <- read.table("../donnees/ozone_simple.txt",header=T,sep=";")
plot(O3 ~ T12, xlim=c(0,35), ylim=c(0,150), data=ozone)
iter <- 1
for(ii in c(1,2,3,9)){
tmp <- polyreg(ozone,d=ii)
lines(tmp$grillex,tmp$grilley,col=iter,lty=iter)
iter <- iter+1
}
legend(15,150,c("d=1","d=2","d=3","d=9"),col=1:4,lty=1:4)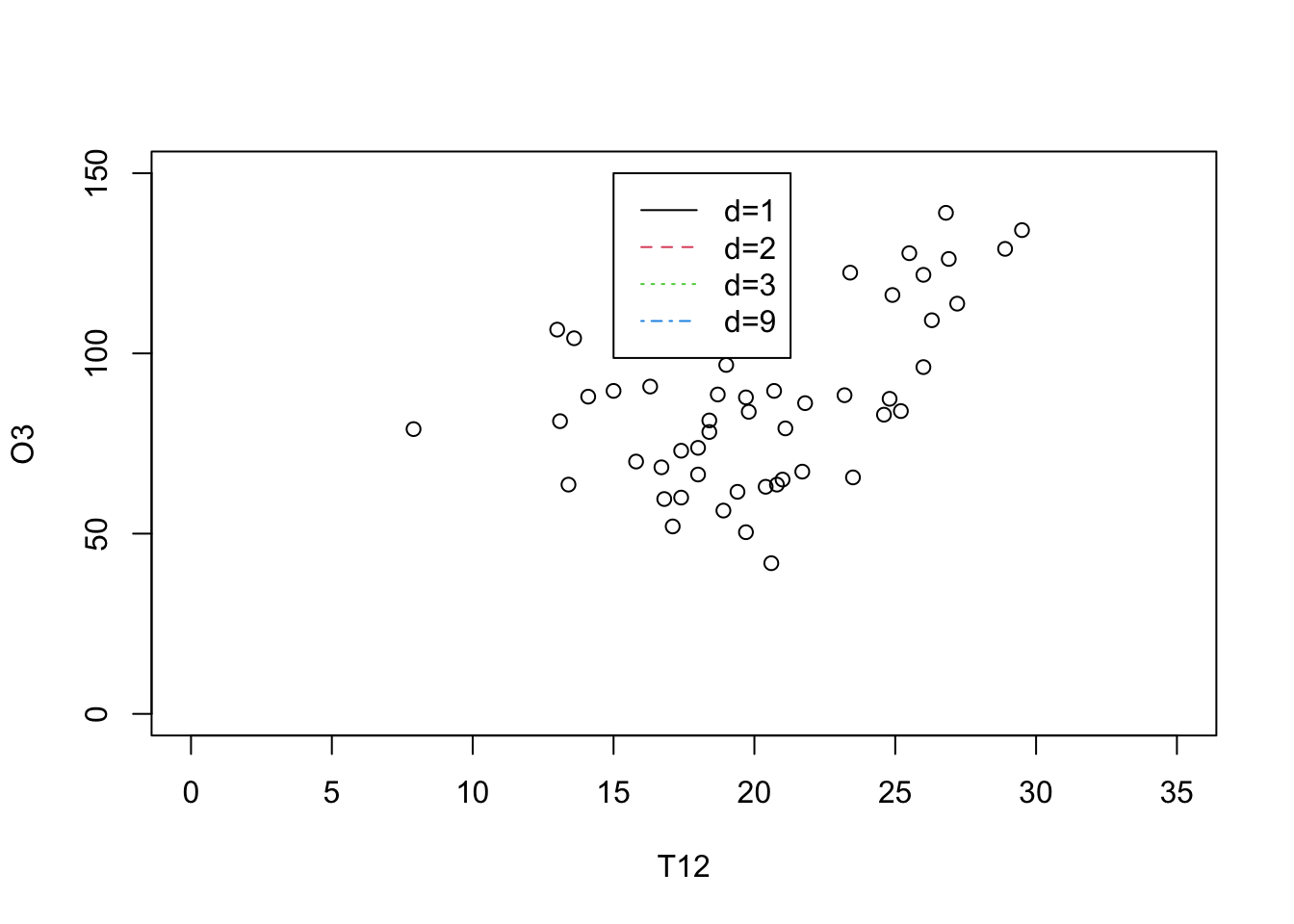
Exercice 4 Considérons la matrice \(X_B\) du plan d’expérience obtenue à partir d’une variable réelle \(X\) transformée dans \(\mathcal{S}_{\xi}^{d+1}\) . Cette matrice est composée des \(d+K+1\) fonction de base notée \(b_j\) et où \(K\) est le nombre de noeuds intérieurs et \(d\) le degré.
Dans le cours, il est indiqué que les fonctions de base \(b_j\) et \(b_{j+d+1}\) en conservant l’ordre des fonctions. Donc \(b_1\) est orthogonale à toutes les fonctions \(b_j\) avec \(j>d+1\), idem pour \(b_2\) avec \(j>d+2\).
En faisant donc le calcul \(X_B'X_B\) on obtient une matrice bande et donc les termes \(a_{ij}\) sont nuls quand \(j>i+d+1\).
On en déduit que les paramètres estimées \(\hat \beta_k\) ne sont pas corrélés avec les \(\hat \beta_j\) dès que \(j>k+d+1\). XB est une matrice bande.