11 Régression logistique

Exercice 1 (Questions de cours)

Exercice 2 (Interprétation des coefficients)

On génère l’échantillon.

n <- 100
set.seed(48967365)
X <- sample(c("A","B","C"),100,replace=TRUE)
Y <- rep(0,n)
set.seed(487365)
Y[X=="A"] <- rbinom(sum(X=="A"),size=1,prob=0.95)
set.seed(4878365)
Y[X=="B"] <- rbinom(sum(X=="B"),size=1,prob=0.95)
set.seed(4653965)
Y[X=="C"] <- rbinom(sum(X=="C"),size=1,prob=0.05)
Y <- factor(Y)
donnees<-data.frame(Y,X)

On ajuste le modèle avec les contraintes par défaut.

model1 <- glm(Y~X,data=donnees,family=binomial)
summary(model1)


Call:
glm(formula = Y ~ X, family = binomial, data = donnees)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   2.2336     0.6075   3.677 0.000236 ***
XB            0.6568     0.9470   0.694 0.487977    
XC           -5.6348     1.1842  -4.758 1.95e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 129.489  on 99  degrees of freedom
Residual deviance:  44.218  on 97  degrees of freedom
AIC: 50.218

Number of Fisher Scoring iterations: 6

On obtient les résultats du test de Wald sur la nullité des paramètres $\beta_0,\beta_2$ et $\beta_3$.

On change la modalité de référence.

model2 <- glm(Y~C(X,base=3),data=donnees,family=binomial)
summary(model2)


Call:
glm(formula = Y ~ C(X, base = 3), family = binomial, data = donnees)

Coefficients:
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)       -3.401      1.017  -3.346  0.00082 ***
C(X, base = 3)A    5.635      1.184   4.758 1.95e-06 ***
C(X, base = 3)B    6.292      1.249   5.035 4.77e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 129.489  on 99  degrees of freedom
Residual deviance:  44.218  on 97  degrees of freedom
AIC: 50.218

Number of Fisher Scoring iterations: 6

On obtient les résultats du test de Wald sur la nullité des paramètres $\beta_0,\beta_1$ et $\beta_2$.

On remarque que dans model1 on accepte la nullité de $\beta_2$ alors qu’on la rejette dans model2. Ceci est logique dans la mesure où ces tests dépendent de la contrainte identifiante choisie. Dans model1 le test de nullité de $\beta_2$ permet de vérifier si $B$ à un effet similaire à $A$ sur $Y$. Dans model2, on compare l’effet de $B$ à celui de $C$. On peut donc conclure $A$ et $B$ ont des effets proches sur $Y$ alors que $B$ et $C$ ont un impact différent. Ceci est logique vu la façon dont les données ont été générées.
Tester l’effet global de $X$ sur $Y$ revient à tester si les coefficients $\beta_1,\beta_2$ et $\beta_3$ sont égaux, ce qui, compte tenu des contraintes revient à considérer les hypothèses nulles :
- $\beta_2=\beta_3=0$ dans model1 ;
- $\beta_1=\beta_2=0$ dans model2.
On peut effectuer les tests de Wald ou du rapport de vraisemblance. On obtient les résultats du rapport de vraisemblance avec :
```
library(car)
Anova(model1,type=3,test.statistic="LR")
```
```
Analysis of Deviance Table (Type III tests)

Response: Y
  LR Chisq Df Pr(>Chisq)    
X   85.271  2  < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
```
Anova(model2,type=3,test.statistic="LR")
```
```
Analysis of Deviance Table (Type III tests)

Response: Y
               LR Chisq Df Pr(>Chisq)    
C(X, base = 3)   85.271  2  < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
On remarque ici que ces deux tests sont identiques : ils ne dépendent pas de la contrainte identifiante choisie.

Exercice 3 (Séparabilité)

On génère l’échantillon demandé.

set.seed(1234)
X <- c(runif(50,-1,0),runif(50,0,1))
set.seed(5678)
Y <- c(rep(0,50),rep(1,50))
df <- data.frame(X,Y)

Le graphe s’obtient avec :

beta <- seq(0,100,by=0.01)
log_vrais <- function(X,Y,beta){
  LV <- rep(0,length(beta))
  for (i in 1:length(beta)){
    Pbeta <- exp(beta[i]*X)/(1+exp(beta[i]*X))
    LV[i] <- sum(Y*X*beta[i]-log(1+exp(X*beta[i])))
#    gradln[i] <- t(Xb)%*%(Yb-Pbeta)
  }
  return(LV)
}
LL <- log_vrais(X,Y,beta)
plot(beta,LL,type="l")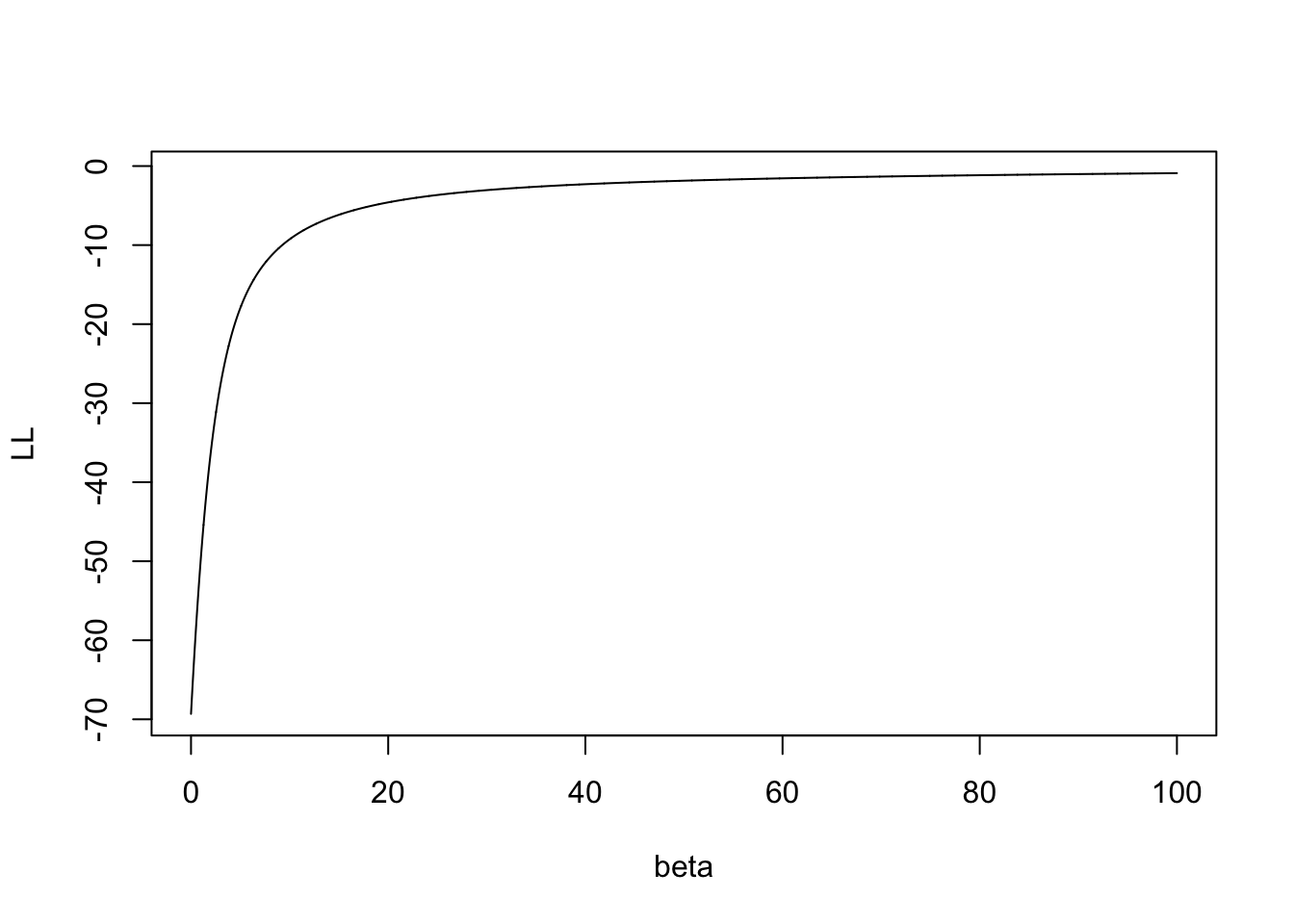

On obtient un avertissement qui nous dit que l’algorithme d’optimisation n’a pas convergé.
```
model <- glm(Y~X-1,data=df,family="binomial")
model$coef
```
```
       X 
1999.371 
```

Le changement proposé supprime la séparabilité des données. On obtient bien un maximum fini pour cette nouvelle vraisemblance.

Y1 <- Y;Y1[1] <- 1
LL1 <- log_vrais(X,Y1,beta)
plot(beta,LL1,type="l")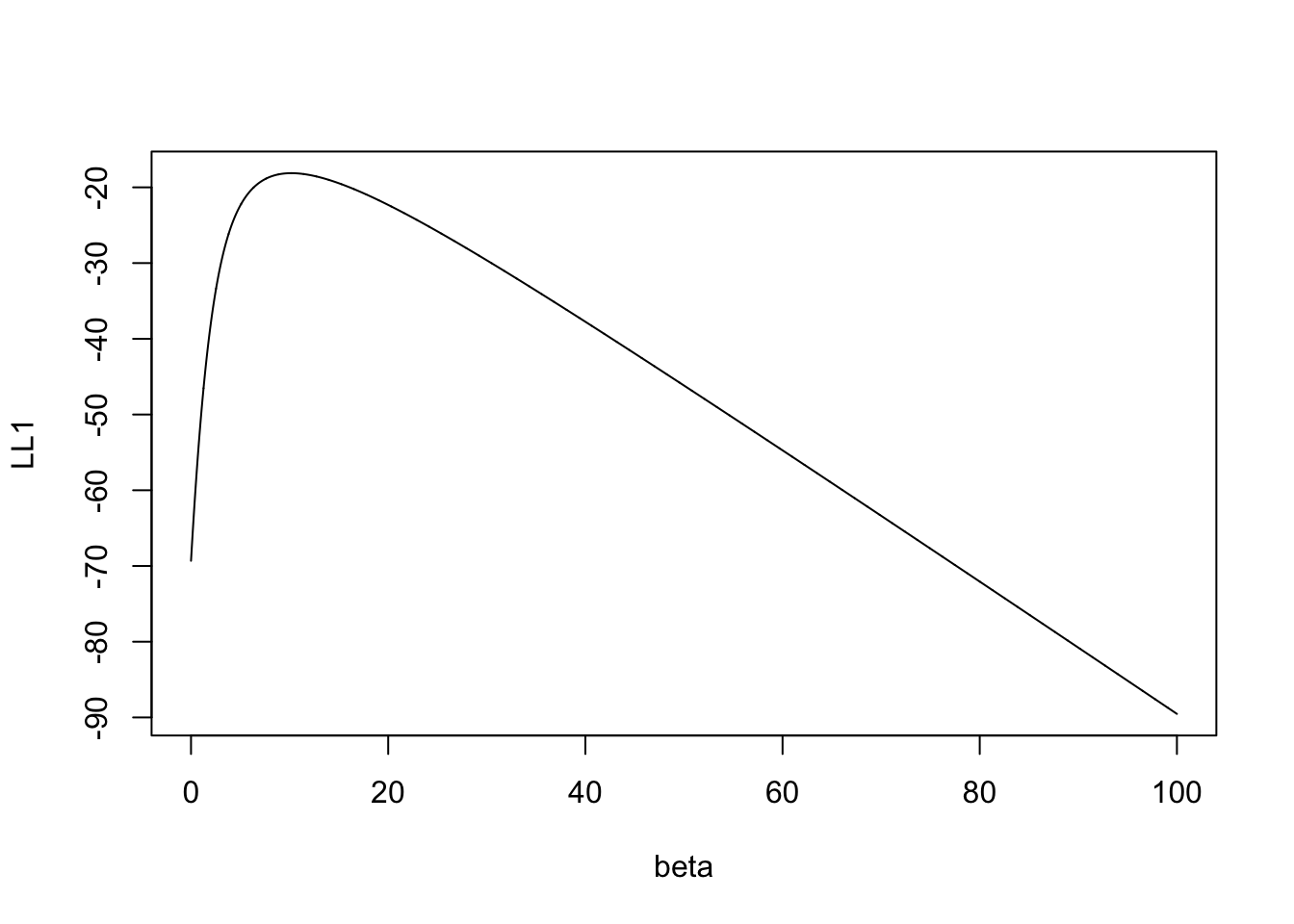

model1 <- glm(Y1~X-1,family="binomial")
model1$coef

       X 
10.17868

Exercice 4 (Matrice hessienne) Le gradient de la log-vraisemblance en $\beta$ est donné par $\nabla \mathcal L(Y,\beta)=X'(Y-P_\beta)$. Sa $j$ème composante vaut \[\frac{\partial\mathcal L}{\partial\beta_j}(\beta)=\sum_{i=1}^nx_{ij}(y_i-p_\beta(x_i)).\]

On peut donc calculer la drivée par rapport à $\beta_\ell$ : \[\begin{align*} \frac{\partial\mathcal L}{\partial\beta_j\partial\beta_\ell}(\beta)= & \frac{\partial}{\partial\beta_\ell}\left[ \sum_{i=1}^nx_{ij}\left(y_i-\frac{\exp(x_i'\beta)}{1+\exp(x_i'\beta)}\right)\right] \\ =& -\sum_{i=1}^nx_{ij}x_{i\ell}\frac{\exp(x_i'\beta)}{[1+\exp(x_i'\beta)]^2} \\ =& -\sum_{i=1}^nx_{ij}x_{i\ell}p_\beta(x_i)(1-p_\beta(x_i)). \end{align*}\] Matriciellement on déduit donc que la hessienne vaut \[\nabla^2\mathcal L(Y,\beta)=-X'W_\beta X,\] où $W_\beta$ est la matrice $n\times n$ diagonale dont le $i$ème terme de la diagonale vaut $p_\beta(x_i)(1-p_\beta(x_i))$. Par ailleurs, comme pour tout $i=1,\dots,n$, on a $p_\beta(x_i)(1-p_\beta(x_i))>0$ et que $X$ est de plein rang, on déduit que $X'W_\beta X$ est définie positive et par conséquent que la hessienne est définie négative.

Exercice 5 (Modèles avec R) On importe les données

panne <- read.table("../donnees/panne.txt",header=T)
head(panne)

  etat age marque
1    0   4      A
2    0   2      C
3    0   3      C
4    0   9      B
5    0   7      B
6    0   6      A

La commande

model <- glm(etat~.,data=panne,family=binomial)
model


Call:  glm(formula = etat ~ ., family = binomial, data = panne)

Coefficients:
(Intercept)          age      marqueB      marqueC  
    0.47808      0.01388     -0.41941     -1.45608  

Degrees of Freedom: 32 Total (i.e. Null);  29 Residual
Null Deviance:      45.72 
Residual Deviance: 43.5     AIC: 51.5

ajuste le modèle \[\log\left(\frac{p_\beta(x)}{1-p_\beta(x)}\right)=\beta_0+\beta_1x_1+\beta_2\mathsf{1}_{x_2=B}+\beta_3\mathsf{1}_{x_2=C}\] où $x_1$ et $x_2$ désigne respectivement les variables age et marque. On obtient les estimateurs avec

coef(model)

(Intercept)         age     marqueB     marqueC 
 0.47808311  0.01388395 -0.41941071 -1.45608147

Il s’agit des tests de Wald pour tester l’effet des variables dans le modèle. Pour l’effet de marque, on va par exemple tester \[H_0:\beta_2=\beta_3=0\quad\text{contre}\quad H_1:\beta_2\neq 0\text{ ou }\beta_3\neq 0.\] Sous $H_0$ la statistique de Wald suit une loi du $\chi^2$ à 4-2=2 degrés de liberté. Pour le test de la variable age le nombre de degrés de liberté manquant est 1. On retrouve cela dans la sortie
```
library(car)
Anova(model,type=3,test.statistic="Wald")
```
```
Analysis of Deviance Table (Type III tests)

Response: etat
            Df  Chisq Pr(>Chisq)
(Intercept)  1 0.3294     0.5660
age          1 0.0218     0.8826
marque       2 1.9307     0.3809
```

Il s’agit cette fois du test du rapport de vraisemblance. Les degrés de liberté manquants sont identiques.

Anova(model,type=3,test.statistic="LR")

Analysis of Deviance Table (Type III tests)

Response: etat
       LR Chisq Df Pr(>Chisq)
age     0.02189  1     0.8824
marque  2.09562  2     0.3507

1. Le modèle s’écrit \[\log\left(\frac{p_\beta(x)}{1-p_\beta(x)}\right)=\beta_0+\beta_1\mathsf{1}_{x_2=A}+\beta_2\mathsf{1}_{x_2=B}.\]
2. Le modèle ajusté ici est \[\log\left(\frac{p_\beta(x)}{1-p_\beta(x)}\right)=\gamma_0+\gamma_1\mathsf{1}_{x_2=B}+\gamma_2\mathsf{1}_{x_2=C}.\] Par identification on a \[\begin{cases} \beta_0+\beta_1=\gamma_0 \\ \beta_0+\beta_2=\gamma_0+\gamma_1 \\ \beta_0=\gamma_0+\gamma_2 \\ \end{cases} \Longleftrightarrow \begin{cases} \beta_0=\gamma_0+\gamma_2 \\ \beta_1=-\gamma_2 \\ \beta_2=\gamma_1-\gamma_2 \\ \end{cases} \Longrightarrow \begin{cases} \widehat\beta_0=-0.92 \\ \widehat\beta_1=1.48 \\ \widehat\beta_2=1.05 \\ \end{cases}\] On peut retrouver ces résultats avec
```
glm(etat~C(marque,base=3),data=panne,family="binomial")
```
```
Call:  glm(formula = etat ~ C(marque, base = 3), family = "binomial", 
    data = panne)

Coefficients:
         (Intercept)  C(marque, base = 3)A  C(marque, base = 3)B  
             -0.9163                1.4759                1.0498  

Degrees of Freedom: 32 Total (i.e. Null);  30 Residual
Null Deviance:      45.72 
Residual Deviance: 43.52    AIC: 49.52
```
Il y a interaction si l’age agit différemment sur la panne en fonction de la marque.
Le modèle ajusté sur R est \[\log\left(\frac{p_\beta(x)}{1-p_\beta(x)}\right)=\delta_0+\delta_1\mathsf{1}_{x_2=B}+\delta_2\mathsf{1}_{x_2=C}+\delta_3x_1+\delta_4x_1\mathsf{1}_{x_2=B}+\delta_5x_1\mathsf{1}_{x_2=C}.\] On obtient ainsi par identification : \[\begin{cases} \alpha_0=\delta_0\\ \alpha_1=\delta_3\\ \beta_0=\delta_0+\delta_1\\ \beta_1=\delta_3+\delta_4\\ \gamma_0=\delta_0+\delta_2\\ \gamma_1=\delta_3+\delta_5 \end{cases}\] On peut ainsi en déduire les valeurs des estimateurs que l’on peut retrouver avec la commande :
```
glm(etat~-1+marque+marque:age,data=panne,family="binomial")
```
```
Call:  glm(formula = etat ~ -1 + marque + marque:age, family = "binomial", 
    data = panne)

Coefficients:
    marqueA      marqueB      marqueC  marqueA:age  marqueB:age  marqueC:age  
    0.23512      0.43375     -2.19633      0.05641     -0.05547      0.27228  

Degrees of Freedom: 33 Total (i.e. Null);  27 Residual
Null Deviance:      45.75 
Residual Deviance: 42.62    AIC: 54.62
```

Exercice 6 (Interprétation)

df <- read.csv("../donnees/logit_ex6.csv")
mod <- glm(Y~.,data=df,family=binomial)
mod1 <- glm(Y~X1,data=df,family=binomial)
summary(mod)


Call:
glm(formula = Y ~ ., family = binomial, data = df)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.57866    0.11926  -4.852 1.22e-06 ***
X1          -0.19471    0.06556  -2.970  0.00298 ** 
X2           0.31899    0.04404   7.244 4.36e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 693.15  on 499  degrees of freedom
Residual deviance: 618.26  on 497  degrees of freedom
AIC: 624.26

Number of Fisher Scoring iterations: 4

summary(mod1)


Call:
glm(formula = Y ~ X1, family = binomial, data = df)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)
(Intercept)  0.001092   0.089499   0.012    0.990
X1          -0.020467   0.051733  -0.396    0.692

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 693.15  on 499  degrees of freedom
Residual deviance: 692.99  on 498  degrees of freedom
AIC: 696.99

Number of Fisher Scoring iterations: 3

On remarque que la nullité du paramètre associé à X1 est accepté dans le modèle avec uniquement X1 alors qu’elle est refusée lorsqu’on considère X1 et X2 dans le modèle.

Exercice 7 (Tests à la main)

Le modèle s’écrit \[log\left(\frac{p_\beta(x)}{1-p_\beta(x)}\right)=\beta_0+\beta_1x.\]

La log vraisemblance s’obtient avec

p <- c(0.76,0.4,0.6,0.89,0.35)
Y <- c(1,0,0,1,1)
L1 <- log(prod(p^Y*(1-p)^(1-Y)))
L1

[1] -2.867909

On calcule les écart-type des estimateurs

X1 <- c(0.47,-0.55,-0.01,1.07,-0.71)
X <- matrix(c(rep(1,5),X1),ncol=2)
W <- diag(p*(1-p))
SIG <- solve(t(X)%*%W%*%X)
sig <- sqrt(diag(SIG))
sig

[1] 1.023252 1.744935

On en déduit les statistiques de test :

beta <- c(0.4383,1.5063)
beta/sig

[1] 0.4283401 0.8632411

On peut faire le test de Wald et du rapport de vraisemblance.

La statistique de test vaut 0.8632411, on obtient donc la probabilité critique

2*(1-pnorm(0.8632411))

[1] 0.3880049

On peut également effectuer un test du rapport de vraisemblance. Le modèle null sans X1 a pour log-vraisemblance

p0 <- 3/5
L0 <- log(prod(p0^Y*(1-p0)^(1-Y)))
L0

[1] -3.365058

La statistique de test vaut donc

2*(L1-L0)

[1] 0.9942984

et la probabilité critique vaut

1-pchisq(2*(L1-L0),df=1)

[1] 0.3186941

On peut retrouver (aux arrondis près) les résultats de l’exercice avec

X <- c(0.47,-0.55,-0.01,1.07,-0.71)
Y <- c(1,0,0,1,1)
df <- data.frame(X,Y)
model <- glm(Y~X,data=df,family="binomial")
logLik(model)

'log Lik.' -2.898765 (df=2)

Anova(model,type=3,test.statistic = "Wald")

Analysis of Deviance Table (Type III tests)

Response: Y
            Df  Chisq Pr(>Chisq)
(Intercept)  1 0.1846     0.6675
X            1 0.7552     0.3848

Anova(model,type=3,test.statistic = "LR")

Analysis of Deviance Table (Type III tests)

Response: Y
  LR Chisq Df Pr(>Chisq)
X  0.93259  1     0.3342

Exercice 8 (Vraisemblance du modèle saturé)

Les variables $(y_t,t=1,\dots,y_T)$ étant indépendantes et de loi binomiales $B(n_t,p_t)$, la log-vraisemblance est donnée par \[\begin{align*} \mathcal L_{\text{sat}}(Y,p)= & \log\left(\prod_{t=1}^T \begin{pmatrix} n_t\\ \tilde y_t \end{pmatrix} p_t^{\tilde y_t}(1-p_t)^{n_t-\tilde y_t}\right) \\ = & \sum_{t=1}^T\left(\log \begin{pmatrix} n_t\\ \tilde y_t \end{pmatrix} +\tilde y_t\log(p_t)+(n_t-\tilde y_t)\log(1-p_t)\right) \end{align*}\]
La dérivée de la log-vraisemblance par rapport à $p_t$ s’écrit \[\frac{\tilde y_t}{p_t}-\frac{n_t-\tilde y_t}{1-p_t}.\] Cette dérivée s’annule pour \[\widehat p_t=\frac{\tilde y_t}{n_t}.\]
On note $\widehat \beta$ l’EMV du modèle logistique et $p_{\widehat\beta}$ le vecteur qui contient les valeurs ajustées $p_{\widehat\beta}(x_t),t=1,\dots,T$. On a pour tout $\beta\in\mathbb R^p$ : \[\mathcal L(Y,\beta)\leq\mathcal L(Y,\widehat\beta)=\mathcal L_{\text{sat}}(Y,p_{\widehat\beta})\leq L_{\text{sat}}(Y,\widehat p_t).\]

Exercice 9 (Intervalle de confiance profilé)

artere <- read.table("../donnees/artere.txt",header=T)
modele <- glm(chd~age,data=artere,family=binomial)
B0 <- coef(modele)
OriginalDeviance <- modele$deviance

```
alpha <- 0.05    
```

stderr <- summary(modele)$coefficients[, "Std. Error"]
delta <- sqrt(qchisq((1-alpha/4),df=1))* stderr[2] /5
grille <- B0[2]+(-10):10*delta

On a \[\begin{align*} \mathcal D_1&=-2(\mathcal L(Y,\hat\beta)-\mathcal L_{sat}) \end{align*}\] Pour celle avec l’offset $K_i=x_i\beta_2^*$ elle vaut \[\begin{align*} \mathcal D_o&=-2(\mathcal L(Y,K,\hat\beta_1)-\mathcal L_{sat}) \end{align*}\] où $\hat \beta_1$ maximise $\mathcal L(Y,K,\hat\beta_1)$ c’est à dire $\mathcal L(Y,K,\hat\beta_1)=l(\beta_2^*)$ et nous avons donc \[\begin{align*} \mathcal D_o - \mathcal D_1= 2(\mathcal L(Y,\hat\beta)-\mathcal L(Y,K,\beta_1)= 2(\mathcal L(Y,\hat\beta)-l(\beta_2^*))=P(\beta_2^*). \end{align*}\]

profil2 <- rep(0,length(grille))
for (k in 1:length(grille)) {
  modeleo <- glm(chd~1,family=binomial,offset=artere[,"age"]*grille[k],data=artere)
  profil2[k] <- modeleo$deviance - OriginalDeviance
}

```
profil <- sign(-10:10)*sqrt(profil2)
```

spline(x=profil,y=grille,xout=c(-sqrt(qchisq(1-alpha,1)),sqrt(qchisq(1-alpha,1))))$y

[1] 0.0669275 0.1620014

confint(modele)

                  2.5 %     97.5 %
(Intercept) -7.72587162 -3.2461547
age          0.06693158  0.1620067