ozone <- read.table("../donnees/ozone.txt", header = T, sep = ";")
modele3 <- lm(O3 ~ T12 + Vx + Ne12, data = ozone)
resume3 <- summary(modele3)
coef3 <- coef(resume3)
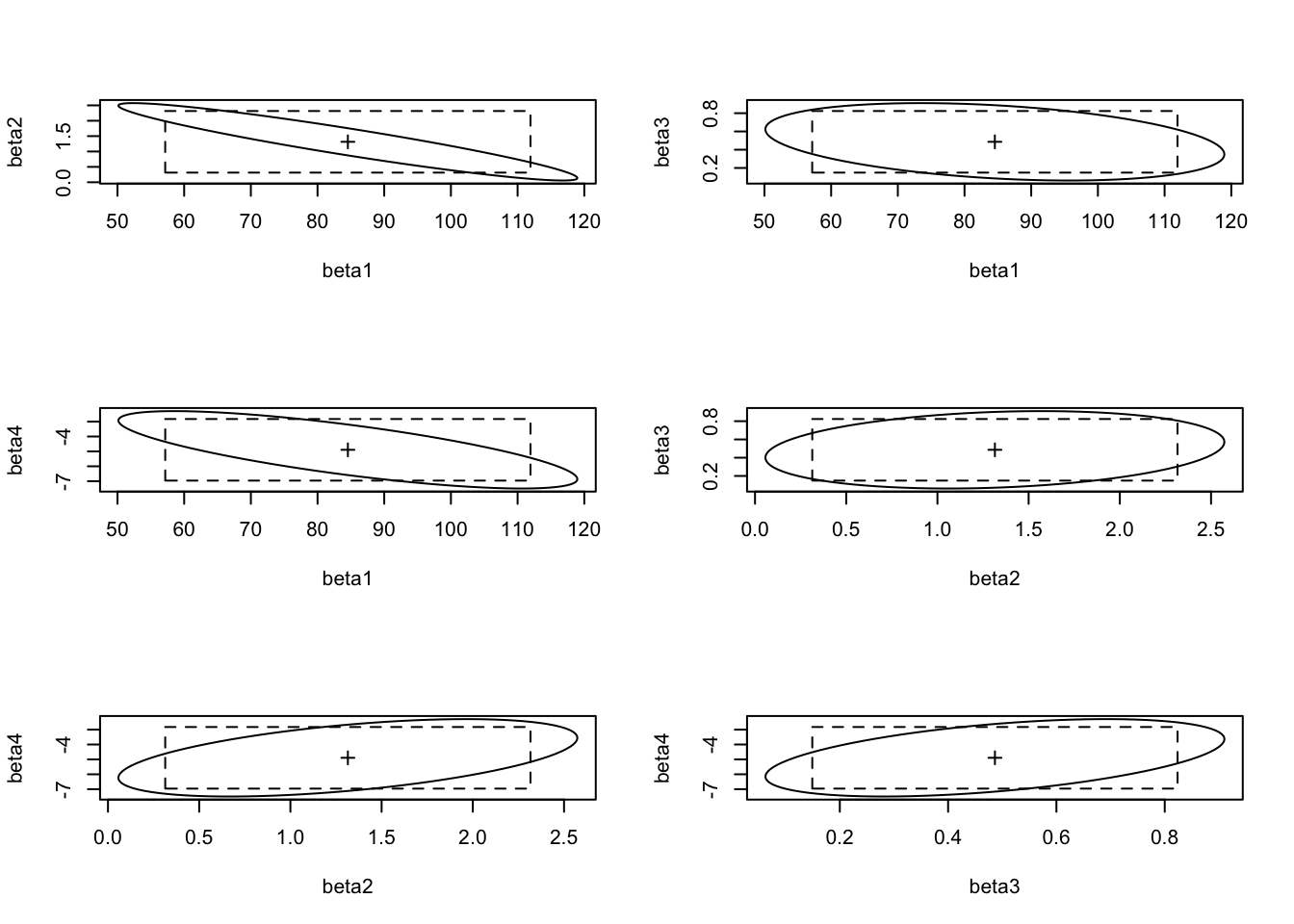
IC3 <- t(confint(modele3, level = 0.95))
IC3 (Intercept) T12 Vx Ne12
2.5 % 57.15842 0.3138112 0.1491857 -6.960609
97.5 % 111.93625 2.3162807 0.8237055 -2.826137library(ellipse)
par(mfrow=c(3,2))
for(i in 1:3){
for(j in (i+1):4){
plot(ellipse(modele3,c(i,j),level=0.95),type="l",
xlab=paste("beta",i,sep=""),ylab=paste("beta",j,sep=""))
points(coef(modele3)[i], coef(modele3)[j],pch=3)
lines(c(IC3[1,i],IC3[1,i],IC3[2,i],IC3[2,i],IC3[1,i]),
c(IC3[1,j],IC3[2,j],IC3[2,j],IC3[1,j],IC3[1,j]),lty=2)
}
}
c(resume3$sigma^2*modele3$df.res/qchisq(0.975,modele3$df.res),
resume3$sigma^2*modele3$df.res/qchisq(0.025,modele3$df.res))[1] 133.6699 305.3706modele3 <- lm(O3 ~ T12 + Vx + Ne12, data = ozone)
resume3 <- summary(modele3)
resume3
Call:
lm(formula = O3 ~ T12 + Vx + Ne12, data = ozone)
Residuals:
Min 1Q Median 3Q Max
-29.0461 -8.4824 0.7861 7.7024 28.2916
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 84.5473 13.6067 6.214 1.38e-07 ***
T12 1.3150 0.4974 2.644 0.01117 *
Vx 0.4864 0.1675 2.903 0.00565 **
Ne12 -4.8934 1.0270 -4.765 1.93e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 13.91 on 46 degrees of freedom
Multiple R-squared: 0.6819, Adjusted R-squared: 0.6611
F-statistic: 32.87 on 3 and 46 DF, p-value: 1.663e-11modele2 <- lm(O3 ~ T12 + Vx, data = ozone)
anova(modele2, modele3)Analysis of Variance Table
Model 1: O3 ~ T12 + Vx
Model 2: O3 ~ T12 + Vx + Ne12
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 13299.4
2 46 8904.6 1 4394.8 22.703 1.927e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1eucalypt <- read.table("../donnees/eucalyptus.txt", header = T, sep = ";")
regsimple <- lm(ht ~ circ, data = eucalypt)
regM <- lm(ht ~ circ + I(sqrt(circ)), data = eucalypt)
anova(regsimple, regM)Analysis of Variance Table
Model 1: ht ~ circ
Model 2: ht ~ circ + I(sqrt(circ))
Res.Df RSS Df Sum of Sq F Pr(>F)
1 1427 2052.1
2 1426 1840.7 1 211.43 163.8 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(regM)
Call:
lm(formula = ht ~ circ + I(sqrt(circ)), data = eucalypt)
Residuals:
Min 1Q Median 3Q Max
-4.1881 -0.6881 0.0427 0.7927 3.7481
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -24.35200 2.61444 -9.314 <2e-16 ***
circ -0.48295 0.05793 -8.336 <2e-16 ***
I(sqrt(circ)) 9.98689 0.78033 12.798 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.136 on 1426 degrees of freedom
Multiple R-squared: 0.7922, Adjusted R-squared: 0.7919
F-statistic: 2718 on 2 and 1426 DF, p-value: < 2.2e-16grille <- data.frame(circ = seq(min(eucalypt[,"circ"]),
max(eucalypt[,"circ"]), len = 100))
ICdte <- predict(regM,new=grille,interval="conf",level=0.95)
ICpre <- predict(regM,new=grille,interval="pred",level=0.95)
plot(ht ~ circ, data = eucalypt, pch="+", col="grey60")
matlines(grille,cbind(ICdte,ICpre[,-1]),lty=c(1,2,2,3,3),col=1)
legend("topleft", lty=2:3, c("E(Y)","Y"))
modele3 <- lm(O3 ~ T12 + Vx + Ne12, data = ozone)resume3 <- summary(modele3)
resume3$coef[,1:2] Estimate Std. Error
(Intercept) 84.5473326 13.6067253
T12 1.3150459 0.4974102
Vx 0.4864456 0.1675496
Ne12 -4.8933729 1.0269960res <- residuals(modele3)
ychap <- predict(modele3)
COEFF <- matrix(0, ncol = 4, nrow = 1000)
colnames(COEFF) <- names(coef(modele3))
ozone.boot <- ozonefor(i in 1:nrow(COEFF)){
resetoile <- sample(res, length(res), replace=T)
O3etoile <- ychap + resetoile
ozone.boot[,"O3"] <- O3etoile
regboot <- lm(formula(modele3), data=ozone.boot)
COEFF[i,] <- coef(regboot)
}apply(COEFF, 2, quantile, probs = c(0.025,0.975)) (Intercept) T12 Vx Ne12
2.5% 59.31069 0.3940245 0.2036312 -6.775764
97.5% 108.67459 2.2270745 0.7974850 -2.900857hist(COEFF[,"T12"], main = "", xlab = "Coefficient de T12")