2 La régression linéaire multiple
Exercice 1 (Question de cours) A, A, B, B, B, C.
Exercice 2 (Covariance de \(\hat\varepsilon\) et \(\hat Y\)) Nous allons montrer que, pour tout autre estimateur \(\tilde{\beta}\) de \(\beta\) linéaire et sans biais, \(\mathop{\mathrm{V}}(\tilde{\beta}) \geq \mathop{\mathrm{V}}(\hat \beta)\). Décomposons la variance de \(\tilde{\beta}\) \[\begin{eqnarray*} \mathop{\mathrm{V}}(\tilde{\beta}) = \mathop{\mathrm{V}}(\tilde{\beta} - \hat \beta+\hat \beta) =\mathop{\mathrm{V}}(\tilde{\beta} - \hat \beta)+\mathop{\mathrm{V}}(\hat \beta) - 2 \mathop{\mathrm{Cov}}(\tilde{\beta} - \hat \beta,\hat \beta). \end{eqnarray*}\] Les variances étant définies positives, si nous montrons que \(\mathop{\mathrm{Cov}}(\tilde{\beta}- \hat \beta,\hat \beta)=0\), nous aurons fini la démonstration.\ Puisque \(\tilde{\beta}\) est linéaire, \(\tilde{\beta} = A Y\). De plus, nous savons qu’il est sans biais, c’est-à-dire \(\mathbf E(\tilde{\beta}) = \beta\) pour tout \(\beta\), donc \(A X = I\). La covariance devient : \[\begin{eqnarray*} \mathop{\mathrm{Cov}}(\tilde{\beta} - \hat \beta,\hat \beta) &=& \mathop{\mathrm{Cov}}(A Y,(X'X)^{-1}X'Y) - \mathop{\mathrm{V}}(\hat \beta)\\ &=& \sigma^2 A X (X'X)^{-1} - \sigma^2 (X'X)^{-1}=0. \end{eqnarray*}\]
Exercice 3 (Théorème de Gauss Markov) Nous devons montrer que, parmi tous les estimateurs linéaires sans biais, l’estimateur de MC est celui qui a la plus petite variance. La linéarité de \(\hat \beta\) est évidente. Calculons sa variance : \[\begin{eqnarray*} \mathop{\mathrm{V}}(\hat \beta) = \mathop{\mathrm{V}}((X'X)^{-1}X'Y) = (X'X)^{-1}X'\mathop{\mathrm{V}}(Y)X(X'X)^{-1}=\sigma^2 (X'X)^{-1}. \end{eqnarray*}\] Nous allons montrer que, pour tout autre estimateur \(\tilde{\beta}\) de \(\beta\) linéaire et sans biais, \(\mathop{\mathrm{V}}(\tilde{\beta}) \geq \mathop{\mathrm{V}}(\hat \beta)\). Décomposons la variance de \(\tilde{\beta}\) \[\begin{eqnarray*} \mathop{\mathrm{V}}(\tilde{\beta}) = \mathop{\mathrm{V}}(\tilde{\beta} - \hat \beta+\hat \beta) =\mathop{\mathrm{V}}(\tilde{\beta} - \hat \beta)+\mathop{\mathrm{V}}(\hat \beta) - 2 \mathop{\mathrm{Cov}}(\tilde{\beta} - \hat \beta,\hat \beta). \end{eqnarray*}\] Les variances étant définies positives, si nous montrons que \(\mathop{\mathrm{Cov}}(\tilde{\beta}- \hat \beta,\hat \beta)=0\), nous aurons fini la démonstration.\ Puisque \(\tilde{\beta}\) est linéaire, \(\tilde{\beta} = A Y\). De plus, nous savons qu’il est sans biais, c’est-à-dire \(\mathbf E(\tilde{\beta}) = \beta\) pour tout \(\beta\), donc \(A X = I\). La covariance devient : \[\begin{eqnarray*} \mathop{\mathrm{Cov}}(\tilde{\beta} - \hat \beta,\hat \beta) &=& \mathop{\mathrm{Cov}}(A Y,(X'X)^{-1}X'Y) - \mathop{\mathrm{V}}(\hat \beta)\\ &=& \sigma^2 A X (X'X)^{-1} - \sigma^2 (X'X)^{-1}=0. \end{eqnarray*}\]
Exercice 4 (Représentation des variables) Nous représentons les données dans \(\mathbb R^2\) pour le premier jeu et dans \(\mathbb R^3\) pour le second.
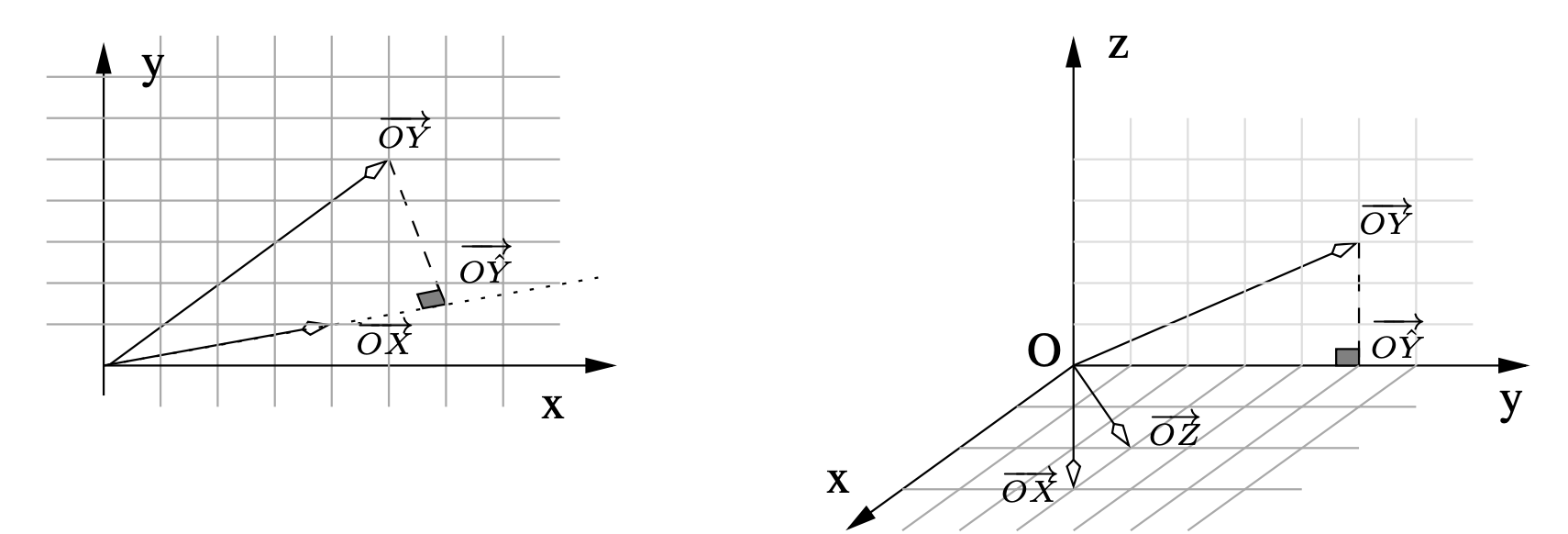
Dans le premier modèle, nous projetons \(Y\) sur l’espace engendré par \(X\), soit la droite de vecteur directeur \(\overrightarrow{OX}\). Nous trouvons par le calcul \(\hat \beta = 1.47\), résultat que nous aurions pu trouver graphiquement car \(\overrightarrow{O \hat Y}= \hat \beta . \overrightarrow{OX}\).
Considérons \(\mathbb R^3\) muni de la base orthonormée \((\vec{i},\vec{j},\vec{k})\). Les vecteurs \(\overrightarrow{OX}\) et \(\overrightarrow{OZ}\) engendrent le même plan que celui engendré par \((\vec{i},\vec{j})\). La projection de \(Y\) sur ce plan donne \(\overrightarrow{O \hat Y}\). Il est quasiment impossible de trouver \(\hat \beta\) et \(\hat \gamma\) graphiquement mais nous trouvons par le calcul \(\hat \beta = -3.33\) et \(\hat \gamma =5\).
Exercice 5 (Modèles emboîtés) Nous obtenons \[\begin{eqnarray*} \hat Y_p = X \hat \beta \quad \hbox{et} \quad \hat Y_q= X_q \hat \gamma. \end{eqnarray*}\] Par définition du \(\mathbb R2\), il faut comparer la norme au carré des vecteurs \(\hat Y_p\) et \(\hat Y_q\). Notons les espaces engendrés par les colonnes de \(X_q\) et \(X\), \(\mathcal M_{X_q}\) et \(\mathcal M_{X}\), nous avons \(\mathcal M_{X_q} \subset \mathcal M_{X}\). Nous obtenons alors \[\begin{eqnarray*} \hat Y_p = P_{X_p}Y = (P_{X_q} + P_{X^{\perp}_q})P_{X_p}Y &=& P_{X_q}P_{X_p}Y + P_{X^{\perp}_q}P_{X_p}Y\\ &=& P_{X_q}Y + P_{X^{\perp}_q \cap X_p} Y\\ &=& \hat Y_q + P_{X^{\perp}_q \cap X_p} Y. \end{eqnarray*}\] En utilisant le théorème de Pythagore, nous avons \[\begin{eqnarray*} \| \hat Y_p \|^2 &=& \|\hat Y_q \|^2 + \| P_{X^{\perp}_q \cap X_p} Y \|^2 \geq \|\hat Y_q \|^2, \end{eqnarray*}\] d’où \[\begin{eqnarray*} \mathbb R2(p)=\frac{\| \hat Y_p \|^2}{\| Y \|^2} \geq \frac{\| \hat Y_q \|^2}{\| Y \|^2} =\mathbb R2(q). \end{eqnarray*}\]
En conclusion, lorsque les modèles sont emboîtés \(\mathcal M_{X_q} \subset \mathcal M_{X}\), le \(\mathbb R2\) du modèle le plus grand (ayant le plus de variables) sera toujours plus grand que le \(\mathbb R2\) du modèle le plus petit.
Exercice 6 La matrice \(X'X\) est symétrique, \(n\) vaut 30 et \(\bar x= \bar z=0\). Le coefficient de corrélation \[\begin{equation*} \rho_{x,z} = \frac{\sum_{i=1}^{30} (x_i -\bar x)(z_i - \bar z)} {\sqrt{\sum_{i=1}^{30} (x_i -\bar x)^2\sum_{i=1}^{30} (z_i - \bar z)^2}} =\frac{\sum_{i=1}^{30} x_i z_i} {\sqrt{\sum_{i=1}^{30} x_i^2 \sum_{i=1}^{30} z_i^2}} =\frac{7}{\sqrt{150}}=0.57. \end{equation*}\] Nous avons \[\begin{eqnarray*} y_i &=& -2 +x_i+z_i+\hat \varepsilon_i \end{eqnarray*}\] et la moyenne vaut alors \[\begin{eqnarray*} \bar y &=& -2 + \bar x +\bar z + \frac{1}{n}\sum_i \hat \varepsilon_i. \end{eqnarray*}\] La constante étant dans le modèle, la somme des résidus est nulle car le vecteur \(\hat \varepsilon\) est orthogonal au vecteur \(\mathbf{1}\). Nous obtenons donc que la moyenne de \(Y\) vaut 2 car \(\bar x=0\) et \(\bar z=0\). Nous obtenons en développant \[\begin{eqnarray*} \|\hat Y \|^2 &=& \sum_{i=1}^{30}(-2+x_i+2z_i)^2\\ &=& 4+10+60+14=88. \end{eqnarray*}\] Par le théorème de Pythagore, nous concluons que \[\begin{eqnarray*} \mathop{\mathrm{SCT}}=\mathop{\mathrm{SCE}}+\mathop{\mathrm{SCR}}=88+12=100. \end{eqnarray*}\]
Exercice 7 (Changement d’échelle des variables explicatives) Nous avons l’estimation sur le modèle avec les variables originales qui minimise \[\begin{align*} \mathop{\mathrm{MCO}}(\beta)&=\|Y - \sum_{j=1}^{p} X_j \beta_j \|^{2} \end{align*}\] Cette solution est notée \(\hat \beta\).
Nous avons l’estimation sur le modèle avec les variables prémultipliées par \(a_{j}\) (changement d’échelle) qui minimise
\[ \begin{align*} \tilde{\mathop{\mathrm{MCO}}}(\beta)&=\|Y - \sum_{j=1}^{p} \tilde X_j \beta_j \|^{2} = \|Y - \sum_{j=1}^{p} a_{j} X_j \beta_j \|^{2}\\ &= \|Y - \sum_{j=1}^{p} X_j \gamma_j \|^{2}=\mathop{\mathrm{MCO}}(\gamma), \end{align*} \]
en posant en dernière ligne \(\gamma_{j}=a_{j} \beta_j\). La solution de de \(\mathop{\mathrm{MCO}}(\gamma)\) (ou encore \(\mathop{\mathrm{MCO}}(\beta)\)) est \(\hat \beta\). La solution de \(\tilde{\mathop{\mathrm{MCO}}}(\beta)\) est alors donnée par \(\hat \beta_{j}=a_{j} \tilde \beta_j\).
Exercice 8 (Différence entre régression multiple et régressions simples)
Calculons l’estimateur des MCO noté traditionnellement \((X'X)^{-1}X'Y\) avec la matrice \(X\) qui possède ici deux colonnes (notées ici \(X\) et \(Z\)) et \(n\) lignes. On a donc \[\begin{align*} (X'X)&= \begin{pmatrix} \|X\|^{2} & <X,Z>\\ <X,Z> & \|Z\|^{2} \\ \end{pmatrix} \end{align*}\] Son déterminant est \(\Delta= \|X\|^{2}\|Z\|^{2} - 2 <X,Z>\) et son inverse est \[\begin{align*} \frac{1}{\Delta} \begin{pmatrix} \|Z\|^{2} & -<X,Z>\\ -<X,Z> & \|X\|^{2} \\ \end{pmatrix} \end{align*}\] Ensuite \(X'Y\) est simplement le vecteur colonne de coordonnées \(<X,Y>\) et \(<Z,Y>\). En rassemblant le tout nous avons \[\begin{align*} \hat \beta_{1}&=\frac{1}{\Delta}(\|Z\|^{2} <X,Y> - <X,Z><Z,Y>),\\ \hat \beta_{2}&=\frac{1}{\Delta}(\|X\|^{2} <Z,Y> - <X,Z><X,Y>). \end{align*}\] Si \(<X,Z>=0\) (les deux vecteurs sont orthogonaux) alors cette écriture se simplifie en \[ \hat \beta_{1}=\frac{<X,Y>}{\|X\|^{2}},\quad \hat \beta_{2}=\frac{<Z,Y>}{\|Z\|^{2}}. \]
Calculons l’estimateur des MCO noté traditionnellement \((X'X)^{-1}X'Y\) avec la matrice \(X\) qui possède ici une colonne (notée ici \(X\)) et \(n\) lignes. On a donc \[\begin{align*} \hat \beta_{X} = \frac{<X,Y>}{\|X\|^{2}}. \end{align*}\] Passons maintenant à la matrice qui possède ici une colonne (notée ici \(Z\)) et \(n\) lignes. On a donc \[\begin{align*} \hat \beta_{Z} = \frac{<Z,Y>}{\|Z\|^{2}}. \end{align*}\]
En général les coefficients des régressions simples ne sont pas ceux obtenus par régression multiple sauf si les variables sont orthogonales.
Nous avons ici les résidus de la première régression qui sont \[\begin{align} \hat \varepsilon = Y - \hat \beta_{X} X. \end{align}\] La deuxième régression (sur les résidus) donne le coefficient \[\begin{align*} \hat \beta_{Z} = \frac{<Z,\hat \varepsilon>}{\|Z\|^{2}} = \hat \beta_{Z} - \hat \beta_{X}\frac{<Z,X>}{\|Z\|^{2}} \end{align*}\] La régression séquentielle donne des coefficients différents des régressions univariées ou bivariées sauf si les variables sont orthogonales. \end{enumerate}
Exercice 9 (TP : différence entre régression multiple et régressions simples)
Simulons 2 variables explicatives avec GNU-R pour \(n=100\) individus selon selon deux loi uniforme \([0,1]\) :
n <- 100 set.seed(4321) # pour fixer les simulations X1 <- runif(n) X2 <- runif(n)Ensuite simulons \(Y\) selon le modèle avec \(\sigma=0.5\)
sigma <- 0.5 set.seed(321) # pour fixer les simulations Y <- 2 -3*X1 + 4*X2 + rnorm(n, sd=sigma) don <- cbind.data.frame(Y,X1,X2) head(don)Y X1 X2 1 4.213477 0.33477802 0.5913398 2 1.602748 0.90913948 0.6715464 3 2.958646 0.41152969 0.5830570 4 3.215113 0.04384097 0.3516151 5 3.367004 0.76350011 0.9298713 6 3.555247 0.75043889 0.9181180Le graphique est obtenu avec
rgl::plot3d(X1,X2,Y)On observe grâce au code ci-dessus que les points sont répartis autour d’un plan (d’équation \(z=2-3x + 4y\)).
Effectuons la régression multiple et stockons \(\hat Y\) dans
Yhat:(regmult <- lm(Y~1+X1+X2, data=don))Call: lm(formula = Y ~ 1 + X1 + X2, data = don) Coefficients: (Intercept) X1 X2 2.080 -2.972 3.827Nous sommes assez proches des coefficients recherchés (2, -3 et 4)
Effectuons les régression simples
(regX1 <- lm(Y~1+X1, data=don))Call: lm(formula = Y ~ 1 + X1, data = don) Coefficients: (Intercept) X1 3.803 -2.441Nous voyons que le paramètre ne correspond pas à celui de \(X_{1}\) dans la régression multiple.
(regX2 <- lm(Y~1+X2, data=don))Call: lm(formula = Y ~ 1 + X2, data = don) Coefficients: (Intercept) X2 0.7221 3.4424Nous voyons que le paramètre ne correspond pas à celui de \(X_{2}\) dans la régression multiple.
Enchainons après la régression simple sur \(X_{1}\) la régression des résidus (ce que \(X_{1}\) n’a pas réussi à modéliser) sur \(X_{2}\):
residX1 <- residuals(regX1) don <- cbind(don, residX1) regX2residX1 <- lm(residX1~1+X2, data=don) regX2residX1Call: lm(formula = residX1 ~ 1 + X2, data = don) Coefficients: (Intercept) X2 -1.965 3.758Là encore le coefficient sur \(X_{2}\) ne correspond pas à celui de \(X_{2}\) dans la régression multiple. :La prévision est différente
(predict(regX2residX1) + predict(regX1))[1:5]1 2 3 4 5 3.242781 2.142450 3.024335 3.051894 3.468733Changeons l’ordre
residX2 <- residuals(regX2) don <- cbind(don, residX2) regX1residX2 <- lm(residX2~1+X1, data=don) regX1residX2Call: lm(formula = residX2 ~ 1 + X1, data = don) Coefficients: (Intercept) X1 1.531 -2.918On a là encore des différences
(predict(regX1residX2) + predict(regX2))[1:5]1 2 3 4 5 3.311895 1.911850 3.059400 3.335703 3.226125Envisageons la covariance empirique
cov(X1,X2)[1] 0.01050429et leur produit scalaire
sum(X1*X2)[1] 28.47696Les deux variables sont loin d’être orthogonales. Centrons les
X1c <- X1 - mean(X1) X2c <- X2 - mean(X2) sum(X1c*X2c)[1] 1.039925Refaisons les régressions: la multiple
donc <- cbind.data.frame(Y,X1c,X2c) (regmultc <- lm(Y~1+X1c+X2c, data=donc))Call: lm(formula = Y ~ 1 + X1c + X2c, data = donc) Coefficients: (Intercept) X1c X2c 2.522 -2.972 3.827Nous retrouvons que seul la constante change puis l’enchainement
(regX1c <- lm(Y~1+X1c, data=donc))Call: lm(formula = Y ~ 1 + X1c, data = donc) Coefficients: (Intercept) X1c 2.522 -2.441Ici les variables \(X_{1c}\) et \(X_{2c}\) étant centrées elles sont orthogonales à la constante. Nous avons donc \[\begin{align} \Im(\mathbf{1}, X_{1c}, X_{2c}) = \Im(\mathbf{1}) \stackrel{\perp}{\oplus} \Im(X_{1c}, X_{2c}) \end{align}\] Le modèle précédent nous donne grâce à l’orthogonalité ci-dessus \(\hat Y_{1c} = P_{\mathbf{1}, X_{1c}}Y=P_{\mathbf{1}}Y + P_{X_{1c}}Y\). Le modèle complet donne de son côté \(\hat Y = P_{\mathbf{1}, X_{1c},X_{2c}}Y=P_{\mathbf{1}}Y + P_{X_{1c},X_{2c}}Y\). Nous retrouvons donc le coefficient constant qui est la coordonnée sur \(\mathbf{1}\) de \(P_{\mathbf{1}}Y\) dans les deux cas.
Enchainons sur la régression sur résidus
residX1c <- residuals(regX1c) donc <- cbind(donc, residX1c) (regX2residX1c <- lm(residX1c~1+X2c, data=don))Call: lm(formula = residX1c ~ 1 + X2c, data = don) Coefficients: (Intercept) X2c 1.669e-16 3.758e+00Puisque le vecteur est \(Y- \hat Y_{1}=Y-P_{\mathbf{1}}Y-P_{X_{1c}}Y\) et que \(X_{2c}\perp\mathbf{1}\) on a la projection des résidus sur \(\Im(\mathbf{1}, X_{2c})\) qui vaut \[\begin{align*} P_{\mathbf{1}, X_{2c}}(Y- \hat Y_{1c})&= P_{\mathbf{1}}(Y- \hat Y_{1c}) + P_{X_{2c}}(Y- \hat Y_{1c})\\ &=P_{\mathbf{1}}Y - P_{\mathbf{1}}P_{\mathbf{1}, X_{1c}}Y + P_{X_{2c}}Y - P_{X_{2c}}P_{\mathbf{1}, X_{1c}}Y\\ &= P_{\mathbf{1}}Y - P_{\mathbf{1}}Y - 0 + P_{X_{2c}}Y - 0 - P_{X_{2c}}P_{X_{1c}}Y\\ &= P_{X_{2c}} Y - P_{X_{2c}}P_{X_{1c}}Y \end{align*}\] Cette dernière somme de projection est dans \(\Im(X_{1c}, X_{2c})\) qui est un sous-espace orthogonal à \(\Im(\mathbf{1})\), d’où le coefficient 0 pour la constante.
Pour les prévisions rien ne change :
predict(regmultc)[1:5]1 2 3 4 5 3.348336 1.948483 3.088559 3.295485 3.369866
Exercice 10 (TP : régression multiple et code R)
ozone <- read.table("../donnees/ozone_complet.txt",sep=";",header=TRUE) nomvar <- names(ozone)(ch <- paste(nomvar[-1],collapse = "+"))[1] "T6+T9+T12+T15+T18+Ne6+Ne9+Ne12+Ne15+Ne18+Vdir6+Vvit6+Vdir9+Vvit9+Vdir12+Vvit12+Vdir15+Vvit15+Vdir18+Vvit18+Vx+maxO3v"(ch2 <- paste("maxO3~",ch,sep=""))[1] "maxO3~T6+T9+T12+T15+T18+Ne6+Ne9+Ne12+Ne15+Ne18+Vdir6+Vvit6+Vdir9+Vvit9+Vdir12+Vvit12+Vdir15+Vvit15+Vdir18+Vvit18+Vx+maxO3v"form <- formula(ch2) lm(form,data=ozone)Call: lm(formula = form, data = ozone) Coefficients: (Intercept) T6 T9 T12 T15 T18 31.628418 -1.937194 0.121834 1.522143 0.609047 0.091871 Ne6 Ne9 Ne12 Ne15 Ne18 Vdir6 0.091969 -0.692891 -0.941925 -0.033847 -0.107068 -0.001344 Vvit6 Vdir9 Vvit9 Vdir12 Vvit12 Vdir15 1.586427 -0.009728 -1.163728 -0.007144 0.182232 -0.003468 Vvit15 Vdir18 Vvit18 Vx maxO3v 0.246885 0.006251 0.560660 0.255474 0.465541
Exercice 11 (Régression orthogonale) Les vecteurs étant orthogonaux, nous avons \(\mathcal M_X = \mathcal M_U \stackrel{\perp}{\oplus} \mathcal M_V\). Nous pouvons alors écrire \[\begin{eqnarray*} \hat Y_X = P_X Y &=& (P_U + P_{U^{\perp}})P_X Y \\ &=& P_U P_X Y + P_{U^{\perp}}P_X Y = P_U Y + P_{U^{\perp}\cap X} Y \\ &=& \hat Y_U + \hat Y_V. \end{eqnarray*}\] La suite de l’exercice est identique. En conclusion, effectuer une régression multiple sur des variables orthogonales revient à effectuer \(p\) régressions simples.
Exercice 12 (Centrage, centrage-réduction et coefficient constant)
Comme la dernière colonne de \(X\), notée \(X_p\) vaut \(\mathbf{1}_n\) sa moyenne empirique vaut \(1\) et la variable centrée issue de \(X_p\) est donc \(X_p -1\times\mathbf{1}_n=\boldsymbol{0}_n\).
Nous avons le modèle sur variable centrée \[ \begin{eqnarray*} \tilde Y&=&\tilde X\tilde \beta+ \varepsilon\\ Y-\bar Y\mathbf{1}_n&=&\sum_{j=1}^{p-1}{(X_j -\bar X_j\mathbf{1}_n)\tilde\beta_j}+\varepsilon\\ Y&=&\sum_{j=1}^{p-1}{\tilde\beta_j X_j}+ \Bigl(\bar Y -\sum_{j=1}^{p-1}{\bar X_j\tilde\beta_j}\Bigr)\mathbf{1}_n+\varepsilon. \end{eqnarray*} \] En identifiant cela donne \[ \begin{eqnarray} \beta_j&=&\tilde\beta_j,\ \forall j\in\{1,\dotsc,p-1\},\nonumber\\ \beta_p&=&\bar Y\mathbf{1}_n-\sum_{j=1}^{p-1}{\bar X_j\tilde\beta_j}. \end{eqnarray} \tag{1}\] Si l’on utilise des variables centrées dans le modèle de régression, on ne met pas de colonne \(\mathbf{1}\) (pas de coefficient constant - intercept). Les coefficients du modèle sur les variables originales sont égaux à ceux sur les variables centrées et le coefficient constant est donné par la formule (équation 1).
Maintenant les variables explicatives sont centrées et réduites : \[\begin{eqnarray*} \tilde Y&=&\tilde X\tilde \beta+ \varepsilon\\ Y-\bar Y\mathbf{1}_n&=&\sum_{j=1}^{p-1}{\frac{(X_j -\bar X_j\mathbf{1}_n)}{\hat\sigma_{X_j}}\tilde\beta_j}+\varepsilon\\ Y&=&\sum_{j=1}^{p-1}{\frac{\tilde\beta_j}{\hat\sigma_{X_j}}X_j}+ \Bigl(\bar Y-\sum_{j=1}^{p-1}{\bar X_j\frac{\tilde\beta_j}{\hat\sigma_{X_j}}}\Bigr)\mathbf{1}_n+\varepsilon. \end{eqnarray*}\] En identifiant cela donne \[\begin{eqnarray*} \beta_j&=&\frac{\tilde\beta_j}{\hat\sigma_{X_j}},\ \forall j\in\{1,\dotsc,p-1\},\\ \beta_p&=&\bar Y\mathbf{1}_n-\sum_{j=1}^{p-1}{\bar X_j\frac{\tilde\beta_j}{\hat\sigma_{X_j}}}. \end{eqnarray*}\] Nous obtenons ici que les coefficients du modèle sur les variables originales sont égaux à ceux sur les variables centrées-réduites divisés par l’écart-type empirique des variables explicatives. Plus la variable explicative \(X_j\) est dispersée, plus son coefficient \(\beta_j\) sera réduit par rapport à \(\tilde\beta_j\). Le coefficient constant est donné par la formule ci-dessus.
La variable à expliquer \(Y\) est elle aussi centrée-réduite~: \[\begin{eqnarray*} \tilde Y&=&\tilde X\tilde \beta+ \tilde\varepsilon\\ \frac{Y-\bar Y\mathbf{1}_n}{\hat\sigma_Y}&=&\sum_{j=1}^{p-1}{\frac{(X_j -\bar X_j\mathbf{1}_n)}{\hat\sigma_{X_j}}\tilde\beta_j}+\tilde\varepsilon\\ Y&=&\hat\sigma_Y\sum_{j=1}^{p-1}{\frac{\tilde\beta_j}{\hat\sigma_{X_j}}X_j}+ \Bigl(\bar Y-\hat\sigma_Y\sum_{j=1}^{p-1}{\bar X_j\frac{\tilde\beta_j}{\hat\sigma_{X_j}}}\Bigr)\mathbf{1}_n+\hat\sigma_Y\tilde\varepsilon. \end{eqnarray*}\] En identifiant cela donne \[\begin{eqnarray*} \beta_j&=&\hat\sigma_Y\frac{\tilde\beta_j}{\hat\sigma_{X_j}},\ \forall j\in\{1,\dotsc,p-1\},\\ \beta_p&=&\bar Y\mathbf{1}_n-\hat\sigma_Y\sum_{j=1}^{p-1}{\bar X_j\frac{\tilde\beta_j}{\hat\sigma_{X_j}}},\\ \varepsilon&=&\hat\sigma_Y\tilde\varepsilon. \end{eqnarray*}\] L’écart-type empirique de \(Y\) entre en jeu et nous constatons que les résidus du modèle “centré-réduit” sont égaux à ceux initiaux divisés par l’écart-type empirique de \(Y\).
Simulons 3 variables explicatives avec GNU-R pour \(n=100\) individus selon une loi uniforme \([0,1]\) et équirépartie sur \([1;10]\):
n <- 100 set.seed(1234) # pour fixer les simulations X1 <- runif(n) X2 <- seq(1, 10, length=100) X3 <- rep(1,n) X <- cbind(X1, X2, X3) head(X)X1 X2 X3 [1,] 0.1137034 1.000000 1 [2,] 0.6222994 1.090909 1 [3,] 0.6092747 1.181818 1 [4,] 0.6233794 1.272727 1 [5,] 0.8609154 1.363636 1 [6,] 0.6403106 1.454545 1Simulons maintenant \(Y\) selon le modèle en fixant par exemple \(\beta=(1, 2, 0.1, -4)'\) et \(\sigma=0.1\)
beta <- c(1, 0.1, -4) sigma <- 0.1 set.seed(12345) # pour fixer les simulations Y <- X%*%beta + rnorm(n, sd=sigma) Y[1:5][1] -3.727744 -3.197663 -3.283474 -3.294698 -2.942132Centrons les variables avec
Ytilde <- scale(Y, scale = FALSE) Ytilde[1:5][1] -0.73976069 -0.20968007 -0.29549076 -0.30671453 0.04585078Xtilde <- scale(X, scale = FALSE) head(Xtilde)X1 X2 X3 [1,] -0.3237939 -4.500000 0 [2,] 0.1848021 -4.409091 0 [3,] 0.1717775 -4.318182 0 [4,] 0.1858822 -4.227273 0 [5,] 0.4234181 -4.136364 0 [6,] 0.2028133 -4.045455 0Et éliminons la dernière colonne de \(\tilde X\)
Xtilde <- Xtilde[, -3]Effectuons les deux régressions en constituant deux data-frames. Nous n’ajoutons pas la constante dans les modèles (
-1) car elle est déjà dans la dernière colonne de \(X\) pour le premier modèle et on ne la souhaite pas pour le second.don <- cbind.data.frame(Y,X) dontilde <- cbind.data.frame(Ytilde,Xtilde) names(dontilde) <- c("Ytilde", "X1tilde", "X2tilde") mod <- lm(Y~-1+X1+X2+X3, data=don) modtilde <- lm(Ytilde~-1+X1tilde+X2tilde, data=dontilde)On retrouve bien que les coefficients des variables centrées ou non sont identiques
coef(mod)X1 X2 X3 1.0225207 0.1030809 -4.0022782et que l’intercept est simplement est bien celui donné dans la formule (équation 1)
mean(don$Y)- sum( coef(modtilde)*colMeans(X[,1:2]))[1] -4.002278Centrons et réduisons les variables explicatives (les 2 premières colonnes de \(X\))
Xtilde <- scale(X[, 1:2], scale = TRUE) head(Xtilde)X1 X2 [1,] -1.1617874 -1.706220 [2,] 0.6630787 -1.671751 [3,] 0.6163456 -1.637282 [4,] 0.6669539 -1.602813 [5,] 1.5192439 -1.568344 [6,] 0.7277037 -1.533875Reconstuisons le data-frame qui a changé et le modèle correspondant
dontilde <- cbind.data.frame(Ytilde,Xtilde) names(dontilde) <- c("Ytilde", "X1tilde", "X2tilde") modtilde <- lm(Ytilde~-1+X1tilde+X2tilde, data=dontilde)Retrouvons les coefficients de départ pour les variables explicatives et pour la constante
mean(don$Y)- sum( coef(modtilde)/apply(X[,-3], 2, sd) * colMeans(X[,1:2]) )[1] -4.002278Centrons et réduisons les variables explicatives et la variable à expliquer
Ytilde <- scale(Y, scale = TRUE) Ytilde[1:5][1] -1.8943177 -0.5369313 -0.7566682 -0.7854091 0.1174109Reconstuisons le data frame qui a changé et le modèle correspondant
dontilde <- cbind.data.frame(Ytilde, Xtilde) names(dontilde) <- c("Ytilde", "X1tilde", "X2tilde") modtilde <- lm(Ytilde~-1+X1tilde+X2tilde, data=dontilde)Retrouvons les coefficients de départ pour les variables explicatives
coef(modtilde)/apply(X[,-3],2,sd)*sd(Y)X1tilde X2tilde 1.0225207 0.1030809et pour la constante
mean(don$Y)- sum( coef(modtilde)/apply(X[,-3], 2, sd) * sd(Y)*colMeans(X[, 1:2]) )[1] -4.002278
Exercice 13 (Moindres carrés contraints)
L’estimateur des MC vaut \[\begin{eqnarray*} \hat \beta = (X'X)^{-1}X'Y, \end{eqnarray*}\]
Calculons maintenant l’estimateur contraint. Nous pouvons procéder de deux manières différentes.
La première consiste à écrire le lagrangien \[\begin{eqnarray*} \mathcal{L} = S(\beta) - \lambda'(R\beta-r). \end{eqnarray*}\] Les conditions de Lagrange permettent d’obtenir un minimum \[\begin{eqnarray*} \left\{ \begin{array}{l} \displaystyle\frac{\partial \mathcal{L}}{\partial \beta} = -2X'Y+2X'X\hat{\beta}_c- R'\hat{\lambda}=0,\\ \displaystyle\frac{\partial \mathcal{L}}{\partial \lambda} = R\hat{\beta}_c-r=0, \end{array} \right. \end{eqnarray*}\] Multiplions à gauche la première égalité par \(R(X'X)^{-1}\), nous obtenons \[\begin{eqnarray*} -2 R(X'X)^{-1}X'Y+2R(X'X)^{-1}X'X \hat{\beta}_c-R(X'X)^{-1}R'\hat{\lambda}&=&0\\ -2 R(X'X)^{-1}X'Y+2R\hat{\beta}_c-R(X'X)^{-1}R'\hat{\lambda}&=&0\\ -2 R(X'X)^{-1}X'Y+2r-R(X'X)^{-1}R'\hat{\lambda}&=&0. \end{eqnarray*}\] Nous obtenons alors pour \(\hat \lambda\) \[\begin{eqnarray*} \hat \lambda = 2 \left[R(X'X)^{-1}R'\right]^{-1}\left[r-R(X'X)^{-1}X'Y\right]. \end{eqnarray*}\] Remplaçons ensuite \(\hat \lambda\) \[\begin{eqnarray*} -2X'Y+2X'X\hat{\beta}_c-R'\hat{\lambda}&=&0\\ -2X'Y+2X'X\hat{\beta}_c-2R'\left[R(X'X)^{-1}R'\right]^{-1}\left[r-R(X'X)^{-1}X'Y\right]&=& 0, \end{eqnarray*}\] d’où nous calculons \(\hat \beta_c\) \[\begin{eqnarray*} \hat \beta_c &=& (X'X)^{-1}X'Y+(X'X)^{-1}R'\left[R(X'X)^{-1}R'\right]^{-1} (r-R\hat \beta)\\ &=& \hat \beta + (X'X)^{-1}R'\left[R(X'X)^{-1}R'\right]^{-1}(r-R\hat \beta). \end{eqnarray*}\] La fonction \(S(\beta)\) à minimiser est une fonction convexe sur un ensemble convexe (contraintes linéaires), le minimum est donc unique.
Une autre façon de procéder consiste à utiliser les projecteurs. Supposons pour commencer que \(r=0\), la contrainte vaut donc \(R\beta=0\). Calculons analytiquement le projecteur orthogonal sur \(\mathcal M_0\). Rappelons que \(\dim(\mathcal M_0)=p-q\), nous avons de plus \[\begin{eqnarray*} R \beta &=& 0 \quad \quad \Leftrightarrow \quad \beta \in Ker(R)\\ R (X'X)^{-1}X'X \beta &=& 0\\ U' X \beta &=& 0\quad \quad \hbox{où} \quad \quad U = X (X'X)^{-1}R'. \end{eqnarray*}\] Nous avons donc que \(\forall \beta \in \ker(R)\), \(U' X \beta = 0\), c’est-à-dire que \(\mathcal M_U\), l’espace engendré par les colonnes de \(U\), est orthogonal à l’espace engendré par \(X\beta\), \(\forall \beta \in \ker(R)\). Nous avons donc que \(\mathcal M_U \perp \mathcal M_0\). Comme \(U=X[(X'X)^{-1}R']\), \(\mathcal M_U \subset \mathcal M_X\). En résumé, nous avons \[\begin{eqnarray*} \mathcal M_U \subset \mathcal M_X \quad \hbox{et} \quad \mathcal M_U \perp \mathcal M_0 \quad \hbox{donc} \quad \mathcal M_U \subset (\mathcal M_X \cap \mathcal M_0^{\perp}). \end{eqnarray*}\] Afin de montrer que les colonnes de \(U\) engendrent \(\mathcal M_X \cap \mathcal M_0^{\perp}\), il faut démontrer que la dimension des deux sous-espaces est égale. Or le rang de \(U\) vaut \(q\) (\(R'\) est de rang \(q\), \((X'X)^{-1}\) est de rang \(p\) et \(X\) est de rang \(p\)) donc la dimension de \(\mathcal M_U\) vaut \(q\). De plus, nous avons vu que \[\begin{eqnarray*} \mathcal M_X = \mathcal M_0 \stackrel{\perp}{\oplus}\left(\mathcal M_0^{\perp} \cap \mathcal M_X \right) \end{eqnarray*}\] et donc, en passant aux dimensions des sous-espaces, nous en déduisons que \(\dim(\mathcal M_0^{\perp} \cap \mathcal M_X )=q\). Nous venons de démontrer que \[\begin{eqnarray*} \mathcal M_U = \mathcal M_X \cap \mathcal M_0^{\perp}. \end{eqnarray*}\] Le projecteur orthogonal sur \(\mathcal M_U=\mathcal M_X \cap \mathcal M_0^{\perp}\) s’écrit \[\begin{eqnarray*} P_{U} = U (U'U)^{-1} U'= X (X'X)^{-1} R' [R(X'X)^{-1}R']^{-1}R(X'X)^{-1}X'. \end{eqnarray*}\] Nous avons alors \[\begin{eqnarray*} \hat Y - \hat Y_0 &=& P_U Y\\ X \hat \beta - X \hat \beta_0 &=& X (X'X)^{-1} R' [R(X'X)^{-1}R']^{-1}R(X'X)^{-1}X'Y\\ &=& X (X'X)^{-1} R [R(X'X)^{-1}R']^{-1}R \hat \beta. \end{eqnarray*}\] Cela donne \[\begin{eqnarray*} \hat \beta_0 = \hat \beta - (X'X)^{-1} R [R(X'X)^{-1}R']^{-1}R \hat \beta. \end{eqnarray*}\] Si maintenant \(r\neq 0\), nous avons alors un sous-espace affine défini par \(\{\beta\in \mathbb R^p : R\beta=r\}\) dans lequel nous cherchons une solution qui minimise les moindres carrés. Un sous-espace affine peut être défini de manière équivalente par un point particulier \(\beta_p \in \mathbb R^p\) tel que \(R\beta_p=r\) et le sous-espace vectoriel associé \(\mathcal M_0^v=\{\beta\in \mathbb R^p : R\beta=0\}\). Les points du sous-espace affine sont alors \(\{\beta_0 \in \mathbb R^p : \beta_0=\beta_p+\beta_0^v, \beta_0^v \in \mathcal M_0^v \quad et \quad \beta_p : R\beta_p=r\}\). La solution qui minimise les moindres carrés, notée \(\hat \beta_0\), est élément de ce sous-espace affine et est définie par \(\hat \beta_0=\beta_p+\hat \beta_0^v\) où \[\begin{eqnarray*} \hat \beta_0^v = \hat \beta - (X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}R\hat \beta. \end{eqnarray*}\] Nous savons que \(R\beta_p=r\) donc \[\begin{eqnarray*} R\beta_p = [R(X'X)^{-1}R'][R(X'X)^{-1}R']^{-1}r \end{eqnarray*}\] donc une solution particulière est \(\beta_p = (X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}r\). La solution \(\hat \beta_0\) qui minimise les moindres carrés sous la contrainte \(R\beta=r\) est alors \[ \begin{align} \hat \beta_0 &= \beta_p+\hat \beta_0^v\\\nonumber &=(X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}r + \hat \beta - (X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}R\hat \beta\\\nonumber &=\hat \beta + (X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}(r-R\hat \beta). \end{align} \tag{2}\]
Calculons l’EQM de \(\hat \beta\) qui vaut selon la formule classique: \[\begin{align*} \mathop{\mathrm{EQM}}&= (\mathbf E(\hat \beta) - \beta) (\mathbf E(\hat \beta) - \beta)' + \mathop{\mathrm{V}}(\hat\beta) \end{align*}\] avec \(\mathbf E(\hat \beta)=\beta\) (sous l’hypothèse que \(Y\) est généré par le modèle de régression) et\(\mathop{\mathrm{V}}(\hat\beta) =\sigma^{2} (X'X)^{-1}\).
Pour l’EQM de \(\hat \beta_0\) qui vaut selon la formule classique: \[\begin{align*} \mathop{\mathrm{EQM}}&= (\mathbf E(\hat \beta_0) - \beta_0) (\mathbf E(\hat \beta_0) - \beta_0)' + \mathop{\mathrm{V}}(\hat\beta_0) \end{align*}\] calculons d’abord \(\mathbf E(\hat \beta_0)\) en utilisant l’équation (équation 2): \[\begin{align*} \mathbf E(\hat \beta_0)&=\mathbf E(\hat \beta) + \mathbf E[(X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}(r-R\hat \beta)]\\ &=\beta + (X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}(r-R\beta) \end{align*}\] puisque \(\hat \beta\) est sans biais. Si nous supposons que le modèle satisfait la contrainte (\(R\beta=r\)) alors là encore le biais est nul.
Calculons maintemant la variance: \[\begin{align*} \mathop{\mathrm{V}}(\hat\beta_0) &= \mathop{\mathrm{V}}[\hat \beta + (X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}(r-R\hat \beta)]\\ &=\mathop{\mathrm{V}}(\hat\beta) + \mathop{\mathrm{V}}[(X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}(r-R\hat \beta)] +\\ &\quad \quad 2\mathop{\mathrm{Cov}}[\hat\beta ; (X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}(r-R\hat \beta)]\\ &= \sigma^{2}V_{X}^{-1} + (\mathrm{II}) + (\mathrm{III}) \end{align*}\] Intéressons nous à la seconde partie \((\mathrm{II})\). Comme \(X\) est déterministe ainsi que \(R\) et \(r\) on a en posant pour alléger \(V_{X}=(X'X)\) (matrice symétrique) \[\begin{align*} (\mathrm{II}) &= V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1} \mathop{\mathrm{V}}(r-R\hat \beta) [RV_{X}^{-1}R']^{-1} R V_{X}^{-1}\\ &= V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1} \mathop{\mathrm{V}}(R\hat \beta)[RV_{X}^{-1}R']^{-1} R V_{X}^{-1}\\ &= V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1} R\sigma^{2}V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1} R V_{X}^{-1}\\ &= \sigma^{2}V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1} R V_{X}^{-1} \end{align*}\] La troisième partie est \[\begin{align*} (\mathrm{III}) &= 2V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1}\mathop{\mathrm{Cov}}[\hat\beta ; (r-R\hat \beta)]\\ &=-2V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1}R\mathop{\mathrm{Cov}}[\hat\beta ;\hat\beta]\\ &= -2V_{X}^{-1}R'[RV_{X}^{-1}R']^{-1}R\sigma^{2}V_{X}^{-1} \end{align*}\] Ce qui donne au final \[\begin{align*} \mathop{\mathrm{V}}(\hat\beta_0) &=\sigma^{2}(X'X)^{-1} - \sigma^{2}(X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}R(X'X)^{-1} \end{align*}\] L’écart entre les 2 variances est donc de \(\sigma^{2}(X'X)^{-1}R'[R(X'X)^{-1}R']^{-1}R(X'X)^{-1}\) qui est une matrice de la forme \(A'A\) donc semi-définie positive.