13 Régularisation de la vraisemblance
Exercice 1 (Questions de cours)
- A, B
- C
- A
- C, D
Exercice 2 (Lasso sur des données centrées réduites)
library(bestglm)
data(SAheart)
SAheart.X <- model.matrix(chd~.,data=SAheart)[,-1]
SAheart.Y <- SAheart$chd
library(glmnet)
mod.lasso <- glmnet(SAheart.X,SAheart.Y,family="binomial",alpha=1)lam.lasso <- mod.lasso$lambda lam <- lam.lasso[50] coef(mod.lasso,s=lam)10 x 1 sparse Matrix of class "dgCMatrix" s1 (Intercept) -6.105111733 sbp 0.006097928 tobacco 0.077763845 ldl 0.169776425 adiposity 0.012176169 famhistPresent 0.902337702 typea 0.037527467 obesity -0.050604210 alcohol . age 0.045476625mu <- apply(SAheart.X,2,mean) sig <- apply(SAheart.X,2,sd) mu.mat <- matrix(rep(mu,nrow(SAheart.X)),nrow=nrow(SAheart.X),byrow=T) sig.mat <- matrix(rep(sig,nrow(SAheart.X)),nrow=nrow(SAheart.X),byrow=T) SAheart.X.cr <- (SAheart.X-mu.mat)/sig.mat mod.lasso1 <- glmnet(SAheart.X.cr,SAheart.Y,family="binomial",alpha=1)lam1 <- mod.lasso1$lambda[50] coef(mod.lasso1,s=lam1)[-1]/sigsbp tobacco ldl adiposity famhistPresent 0.006097928 0.077763845 0.169776425 0.012176169 0.902337702 typea obesity alcohol age 0.037527467 -0.050604210 0.000000000 0.045476625
Exercice 3 (Comparaison de méthodes et courbes ROC)
On importe les données et on les sépare en un échantillon d’apprentissage et de test.
df <- read.csv("../donnees/logit_ridge_lasso.csv") set.seed(1254) perm <- sample(nrow(df)) dapp <- df[perm[1:300],] dtest <- df[perm[301:500],]On construit les modèles demandés sur les données d’apprentissage uniquement.
logit <- glm(Y~.,data=dapp,family="binomial") logit.step <- step(logit,direction="backward",trace=0)Xapp <- model.matrix(Y~.,data=dapp)[,-1] Xtest <- model.matrix(Y~.,data=dtest)[,-1] Yapp <- dapp$Y Ytest <- dtest$Ylasso1 <- cv.glmnet(Xapp,Yapp,family="binomial",alpha=1) ridge1 <- cv.glmnet(Xapp,Yapp,family="binomial",alpha=0,lambda=exp(seq(-6,-1,length=100))) lasso2 <- cv.glmnet(Xapp,Yapp,family="binomial",alpha=1,type.measure = "auc") ridge2 <- cv.glmnet(Xapp,Yapp,family="binomial",alpha=0,type.measure = "auc",lambda=exp(seq(-3,2,length=100)))library(tidyverse) score <- data.frame(logit=predict(logit,newdata=dtest,type="response"), step=predict(logit.step,newdata=dtest,type="response"), lasso1=as.vector(predict(lasso1,type="response",newx=Xtest)), ridge1=as.vector(predict(ridge1,type="response",newx=Xtest)), lasso2=as.vector(predict(lasso2,type="response",newx=Xtest)), ridge2=as.vector(predict(ridge2,type="response",newx=Xtest))) %>% mutate(obs=Ytest) %>% gather(key="Methode",value="score",-obs)library(plotROC) ggplot(score)+aes(m=score,d=obs,color=Methode)+geom_roc()+theme_classic()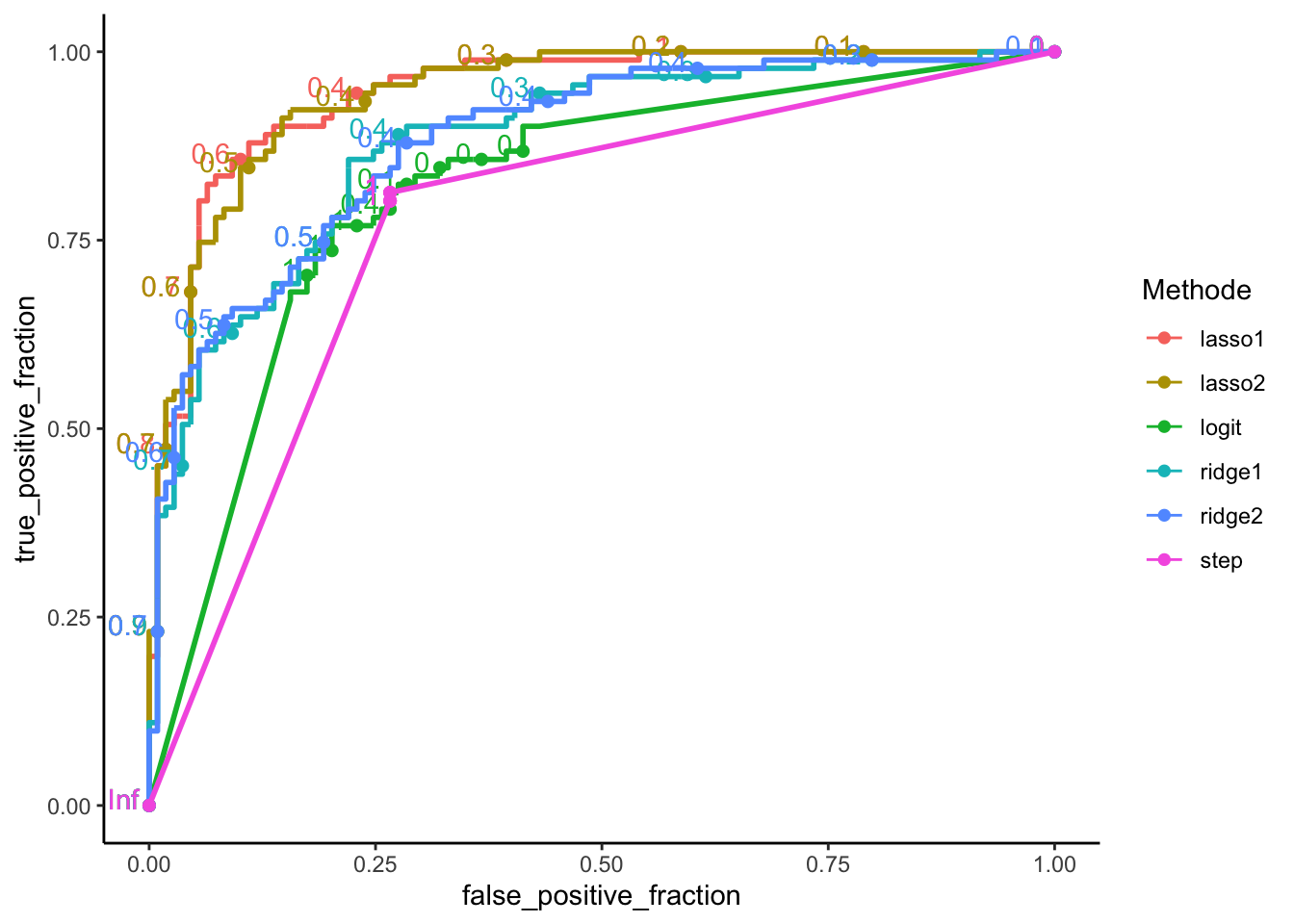
library(tidymodels) score %>% group_by(Methode) %>% mutate(obs=as.factor(obs)) %>% roc_auc(obs,score,event_level = "second") %>% select(Methode,.estimate) %>% arrange(desc(.estimate))# A tibble: 6 × 2 Methode .estimate <chr> <dbl> 1 lasso1 0.945 2 lasso2 0.944 3 ridge2 0.883 4 ridge1 0.880 5 logit 0.816 6 step 0.772
Exercice 4 (Surapprentissage)
score.app <- data.frame(logit=predict(logit,newdata=dapp,type="response"), step=predict(logit.step,newdata=dapp,type="response"), lasso1=as.vector(predict(lasso1,type="response",newx=Xapp)), ridge1=as.vector(predict(ridge1,type="response",newx=Xapp)), lasso2=as.vector(predict(lasso2,type="response",newx=Xapp)), ridge2=as.vector(predict(ridge2,type="response",newx=Xapp))) %>% mutate(obs=Yapp) %>% gather(key="Methode",value="score",-obs)On prédit 1 si la probabilité que Y soit égale à 1 est supérieure ou égale à 0.5 :
prev.app <- score.app %>% mutate(prev=round(score)) prev.app %>% group_by(Methode) %>% summarise(Err=mean(prev!=obs)) %>% arrange(Err)# A tibble: 6 × 2 Methode Err <chr> <dbl> 1 logit 0 2 step 0 3 ridge1 0.0567 4 ridge2 0.0767 5 lasso1 0.0967 6 lasso2 0.11On fait de même avec l’échantillon test.
prev.test <- score %>% mutate(prev=round(score)) prev.test %>% group_by(Methode) %>% summarise(Err=mean(prev!=obs)) %>% arrange(Err)# A tibble: 6 × 2 Methode Err <chr> <dbl> 1 lasso1 0.12 2 lasso2 0.13 3 ridge1 0.215 4 ridge2 0.215 5 step 0.23 6 logit 0.24Sur les données d’apprentissage ce sont les modèles logistiques complets et construits avec step qui ont les plus petites erreurs. Ces modèles souffrent de sur-apprentissage : ils ajustent très bien les données d’apprentissage mais ont du mal à bien prédire de nouveaux individus.